The MD5 algorithm (with examples)

MD5 algorithm with examples

This article covers the mechanics of the MD5 algorithm in detail. It’s our second and final piece on the MD5 hash function, which is an older and insecure algorithm that turns data of random lengths into fixed 128-bit hashes. Our What is MD5? article focused on MD5’s:

Background
History
Applications
Security problems

This time, we’ll be zeroing in on what actually happens when data goes through the MD5 hashing algorithm. How does something like “They are deterministic” (this is just a random sentence we used in the other article) get turned into a 128-bit hash like this?

23db6982caef9e9152f1a5b2589e6ca3

How does the MD5 algorithm work?

Let’s show how the MD5 algorithm works through an example. Our input, “They are deterministic”, becomes wildly different when it is put through the MD5 hash function. All we can guarantee is that it will be 128 bits long, which works out to 32 characters. But how can the MD5 algorithm take inputs of any length, and turn them into seemingly random, fixed-length strings?

Converting the data to binary

When we put “They are deterministic” into an MD5 hash function, the first thing that happens is that it is converted to binary. This is done according to the American Standard Code for Information Interchange (ASCII), which is basically a standard that we use to convert human readable text into the binary code that computers can read.

Using an ASCII table, we see that a capital letter “T” is written as “01010100” in binary. A lowercase “h” is “01101000”, a lowercase “e” is “01100101”, and a lowercase “y” is “01111001”. The binary code for a space (SP) is “00100000”. You can see it in the table at the top of the second column, in line with the decimal number 32.

If we continue on in this fashion, we see that our input, “They are deterministic” is written in binary as:

01010100 01101000 01100101 01111001 00100000 01100001 01110010 01100101 00100000 01100100 01100101 01110100 01100101 01110010 01101101 01101001 01101110 01101001 01110011 01110100 01101001 01100011

Padding in the MD5 algorithm

The next step in MD5 is to add padding. Inputs in MD5 are broken up into 512-bit blocks, with padding added to fill up the rest of the space in the block. Our input is 22 characters long including spaces, and each character is 8 bits long. This means that the input totals 176 bits. With an input of only 176 bits and a 512-bit block that needs to be filled, we need 336 bits of padding to complete the block.

MD5’s padding scheme seems quite strange. After laying out the initial 176 bits of binary that represent our input, the rest of the block is padded with a single one, then enough zeros to bring it up to a length of 448 bits. So:

448 – 1 – 176 = 271

Therefore the padding for this block will include a one, then an extra 271 zeros. The reason we only need to pad it up to 448 bits (instead of 512) is because the final 64 bits (512 – 64 = 448) are reserved to display the message’s length in binary. In this case, the number 176 is 10110000 in binary. This forms the very end of the padding scheme, while the preceding 56 bits (64 minus the eight bits that make up 10110000) are all filled up with zeros.

In cases where the message length takes up a greater number of bits, there will be fewer zeros. If the initial input’s length is longer than 64 bits (if it is greater than 264, which equals 18,446,744,073,709,551,616 in decimal), then only the least significant 64 bits are used.

The term “least significant bits” essentially means the rightmost numbers. As an example, if we only wanted the four least significant bits of a random binary number like 01011110, we would be referring to the 1110 and disregarding the initial 0101.

Once the padding scheme is complete, we end up with the following 512-bit string:

01010100 01101000 01100101 01111001 00100000 01100001 01110010 01100101 00100000 01100100 01100101 01110100 01100101 01110010 01101101 01101001 01101110 01101001 01110011 01110100 01101001 01100011 10000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 10110000

The first 176 bits (the length varies according to the initial input) represent our initial input of “They are deterministic” in binary. The next 272 bits are a one followed by 271 zeros. The final 64 bits are the length of our initial input (176 bits), written in binary. It is preceded by zeros to fill the rest of the 64 bits. The three components of the padded input have been broken up between bold and regular text to make it easier to see where each begins and ends.

Inputs larger than 512 bits

When the initial input is greater than 448 bits long, it is split into multiple 512-bit blocks. Each block includes 512 bits of input data until the entire input has been split into blocks. The final block must include at least 1 bit of padding, plus the 64-bit length in binary.

In the case where the remaining input data is exactly 448 bits long, an entire extra block would need to be added for the padding. The second-last block would include the final 448 bits of data, then a one, followed by 63 zeros to fill up the block. The final block would include 448 zeros (making a total of 512 bits of padding), followed by the 64-bit message length in binary.

If there were 449 remaining bits of input data instead, an extra block would still have to be added. The second last block would include the 449 bits of the remaining input data, followed by a one and 62 zeros to fill up the block. The final block would contain 448 zeros, followed by the 64-bit message length.

In contrast, if the remaining data was only 447 bits long, the final block would include the last 447 bits of input data, followed by a single one as the padding, without any zeros. The 64-bit message length would be appended at the end to bring the total to 512 bits.

The difference between these two cases may seem strange, but it allows the input to be padded by at least one digit, while still leaving room for the 64-bit message length.

The main MD5 algorithm

Here stands the main MD5 algorithm in all its glory:

Don’t understand what’s going on? That’s fine. It’s a complicated algorithm, so there isn’t really any way to draw it without it being confusing.

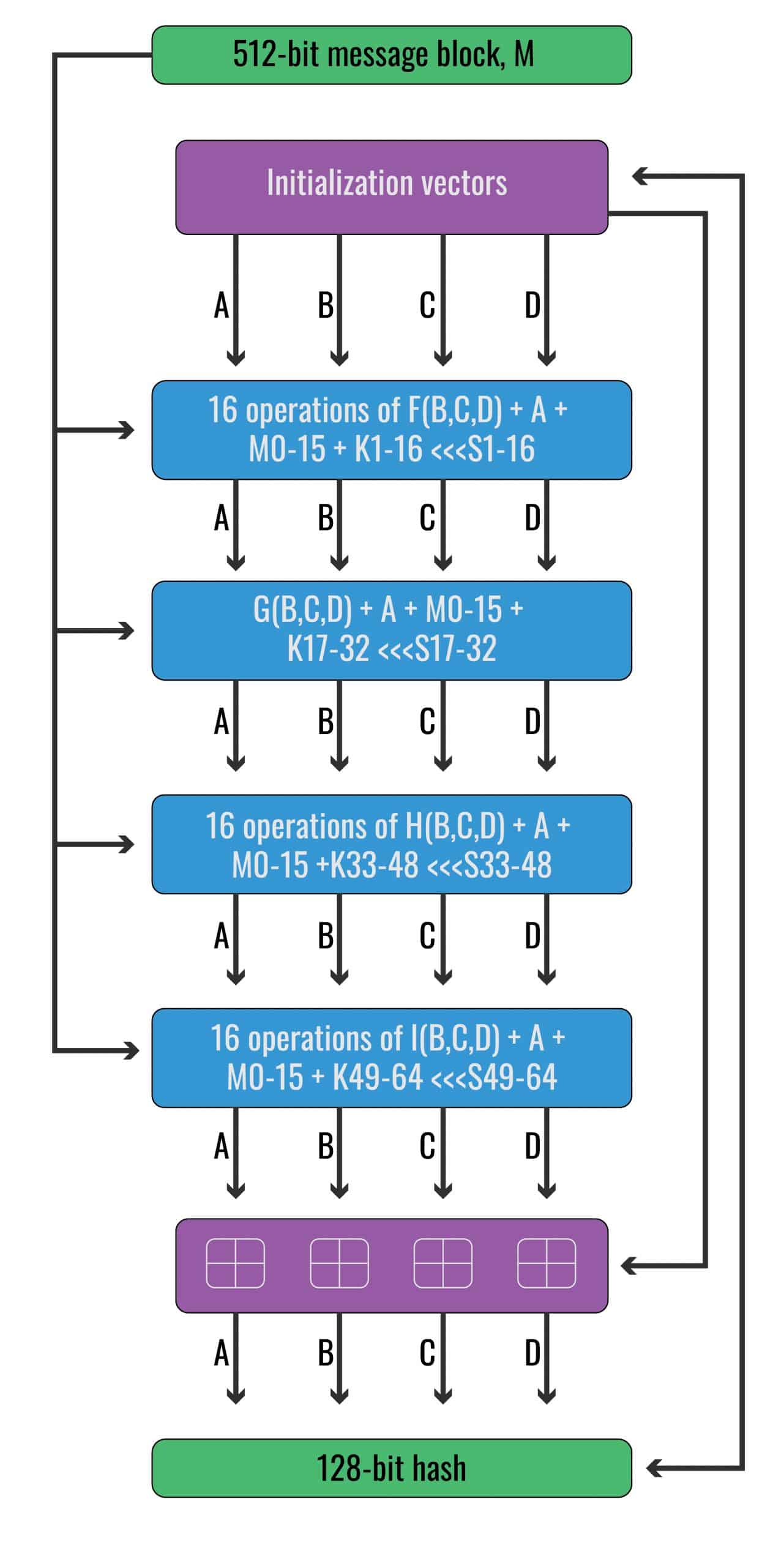
The input M

At the top, we have our input, which says 512-bit message block, M. At this stage of the diagram, it already includes all of the padding that we added in the last step. If you follow the arrow down, you will see that it enters each of the four “16 operations of…” rectangles. Each of these four rectangles are called rounds, and each of them are composed of a series of sixteen operations

This means that our input, M, is an input in each of these four stages. However, before it can be used as an input, our 512-bit M needs to be split into sixteen 32-bit “words”. Each of these words is assigned its own number, ranging from M0 to M15. In our example, these 16 words are:

M₀ – 01010100 01101000 01100101 01111001
M₁– 00100000 01100001 01110010 01100101
M₂ – 00100000 01100100 01100101 01110100
M₃ – 01100101 01110010 01101101 01101001
M₄ – 01101110 01101001 01110011 01110100
M₅ – 01101001 01100011 10000000 00000000
M₆ – 00000000 00000000 00000000 00000000
M₇ – 00000000 00000000 00000000 00000000
M₈ – 00000000 00000000 00000000 00000000
M₉ – 00000000 00000000 00000000 00000000
M₁₀ – 00000000 00000000 00000000 00000000
M₁₁ – 00000000 00000000 00000000 00000000
M₁₂ – 00000000 00000000 00000000 00000000
M₁₃ – 00000000 00000000 00000000 00000000
M₁₄ – 00000000 00000000 00000000 00000000
M₁₅ – 00000000 00000000 00000000 10110000

We will mostly be using hexadecimal for the rest of the article. If you aren’t clear on what hexadecimal is, refer to this section of our prior article on MD5. Using an online converter, the hexadecimal equivalents to our binary numbers are:

M₀ – 54686579
M₁– 20617265
M₂ – 20646574
M₃ – 65726D69
M₄ – 6E697374
M₅ – 69638000
M₆ – 00000000
M₇ – 00000000
M₈ – 00000000
M₉ – 00000000
M₁₀ – 00000000
M₁₁ – 00000000
M₁₂ – 00000000
M₁₃ – 00000000
M₁₄ – 00000000
M₁₅ – 000000B0

Each of these sixteen values act as inputs to the complex set of operations that are represented by each “16 operations of…” rectangle. Once again, these four “16 operations of…” rectangles represent the four different rounds, with the one at the top representing the first round, while the lowest one is the fourth round. While each of these M inputs are used in every single round, they are added in different orders.

In the first round, the M inputs are added into the algorithm sequentially, e.g. M0, M1, M2… M15.

In the second round, the M inputs are added in the following order:

M1, M6, M11, M0, M5, M10, M15, M4, M9, M14, M3, M8, M13, M2, M7, M12

In the third round, the M inputs are added in this sequence:

M5, M8, M11, M14, M1, M4, M7, M10, M13, M0, M3, M6, M9, M12, M15, M2

In the fourth round, the M inputs are added in the following order:

M0, M7, M14, M5, M12, M3, M10, M1, M8, M15, M6, M13, M4, M11, M2, M9

In cases where the initial input and its padding are greater than one 512-bit block, the numbering scheme resets. Once the first block of data has been processed, the second block’s inputs are also labelled M0 through to M15

For simplicity, our example will stick to a single 512-bit block of data that contains 16 words.

The MD5 algorithm’s initialization vectors

Now that we have explained our M inputs a little, it’s time to turn our attention to the Initialization Vectors, which are shown just below the 512-bit message block, M in the diagram.

At the beginning, the initialization vectors are four separate numbers, specified in the RFC that outlines the MD5 standard. These are:

A – 01234567
B – 89abcdef
C – fedcba98
D – 76543210

As we progress through the algorithm, these numbers will be replaced by various outputs that we produce through the calculations. However, these four initialization vectors are important for getting us started. All four of them are inputs into the first “16 operations of…” rectangle.

The MD5 F, G, H and I functions

The first step in the “16 operations of…” rectangle is the function:

F(B, C, D) = (B∧C)∨(¬B∧D)

Looks confusing? We will explain it in depth later on. The important thing to note is that initialization vectors B, C and D are used in this function as inputs.

In the latter stages of the algorithm, the values that replace initialization vectors B, C and D will fill their role.

The F(B, C, D) function is used for the 16 operations of the first round. In the subsequent rounds, its place is taken by these functions:

Round 2: G(B, C, D) = (B∧D)∨(C∧¬D)

Round 3: H(B, C, D) =B⊕C⊕D

Round 4: I(B, C, D) = C⊕(B∨¬D)

Don’t worry, we will explain these too.

The operations

This diagram gives a rough overview of what happens within each “16 operations of…” rectangle:

When we zoom in on each “16 operations of…” rectangle, you can see that the arrows from B, C and D point to a box labelled F. This represents function F(B, C, D) – note that in the other three rounds, the F function is replaced by the G, H and I functions, respectively.

If you follow the arrow out of it into the next box, this indicates that the output of F(B, C, D) is added to the initialization vector A, with a special type of addition. In the first operation, initialization vector A’s value is 01234567, but it changes in subsequent operations.

The result moves onto the next box, where it is added to a portion of the input, represented by Mi. After this, a constant, K, is added to the result, using the same special type of addition. The values for K are is derived from the formula:

abs(sin(i+ 1))×2³²

This formula isn’t too important for understanding the rest of MD5. However, we do need the values it leads to, which are:

K1 – D76AA478
K2 – E8C7B756
K3 – 242070DB
K4 – C1BDCEEE
K5 – F57COFA
K6 – 4787C62A
K7 – A8304613
K8 – FD469501
K9 – 698098D8
K10 – 8B44F7AF
K11 – FFFF5BB1
K12 – 895CD7BE
K13 – 6B901122
K14 – FD987193
K15 – A679438E
K16 – 49B40821
K17 – F61E2562
K18 – C040B340
K19 – 265E5A51
K20 – E9B6C7AA
K21 – D62F105D
K22 – 02441453
K23 – D8A1E681
K24 – E7D3FBC8
K25 – 21E1CDE6
K26 – C33707D6
K27 – F4D50D87
K28 – 455A14ED
K29 – A9E3E905
K30 – FCEFA3F8
K31 – 676F02D9
K32 – 8D2A4C8A
K33 – FFFA3942
K34 – 8771F681
K35 – 699D6122
K36 – FDE5380C
K37– A4BEEA44
K38 – 4BDECFA9
K39 – F6BB4B60
K40 – BEBFBC70
K41 – 289B7EC6
K42 – EAA127FA
K43 – D4EF3085
K44 – 04881D05
K45 – D9D4D039
K46 – E6DB99E5
K47 – 1FA27CF8
K48 – C4AC5665
K49 – F4292244
K50 – 432AFF97
K51 – AB9423A7
K52 – FC93A039
K53 – 655B59C3
K54 – 8F0CCC92
K55 – FFEFF47D
K56 – 85845DD1
K57 – 6FA87E4F
K58 – FE2CE6E0
K59 – A3014314
K60 – 4E0811A1
K61 – F7537E82
K62 – BD3AF235
K63 – 2AD7D2BB
K64 – EB86D391

One of these K values is used in each of the 64 operations for a 512-bit block. K1 to K16 are used in the first round, K17 to K32 are used in the second round, K33 to K48 are used in the third round, and K49 to K64 are used in the fourth round.

After the K value has been added, the next step is to shift the number of bits to the left by a predefined amount, Si. We will explain how this works further on in the article. The amount that each bit is shifted varies according to which operation the MD5 algorithm is up to. Each operation has a preset number of shifts, and the operations use them in sequential order (e.g. S1, S2, S3, etc.). The S values are:

Round one
- S1, S5, S9, S13 – 7
- S2, S6, S10, S14 – 12
- S3, S7, S11, S15 – 17
- S4, S8, S12, S16, – 22

Round two
- S17, S21, S25, S29 – 5
- S18, S22, S26, S30 – 9
- S19, S23, S27, S31 – 14
- S20, S24, S28, S32 – 20

Round three
- S33, S37, S41, S45 – 4
- S34, S38, S42, S46 – 11
- S35, S39, S43, S47 – 16
- S36, S40, S44, S48 – 13

Round four
- S49, S53, S57, S61 – 6
- S50, S54, S58, S62 – 10
- S51, S55, S59, S63 – 15
- S52, S56, S60, S64 – 21

After the shift has been made, the result of all of these calculations is added to the value for initialization vector B. Initially, it’s 89abcdef, but it changes in subsequent operations.

The output of this value becomes the initialization vector for B in the next operation. The initialization vectors B, C and D are shuffled over one space to the right, so that B becomes C, C becomes D, and D becomes A in the next operation.

Four rounds of 16 operations

This process goes in a loop for 16 operations. Each time, the inputs stipulated above are used for their respective operation. The 17th operation is the start of the second round, and the process continues similarly, except the G function is used instead.

Things change again by the 33rd operation, when the H function is used for the duration of the third round. The fourth round begins at the 49th operation, and the I function is used instead.

Upon conclusion of the fourth round and its 64th operation, the outputs are added to the original initialization vectors that we listed above. The result of this calculation is the final MD5 hash of our input.

Confused?

It’s okay, we have begun with a rough and simplistic overview that only aims to give you an outline of the many steps involved in MD5. In the next section, we will walk through each part of the process in greater detail

The MD5 algorithm in-depth

Let’s start by digging into the F function.

The F function

The F function is a bitwise operation (so are functions G, H and I). These are basically fast and easy ways for computers to perform arithmetic with binary. While computers do their work in binary, we will mostly be sticking to hexadecimal because it’s easier to read. Refer to the section on hexadecimal in our other article on MD5 if you need a deeper understanding on what it is.

The F function is:

F(B, C, D) = (B∧C)∨(¬B∧D)

If you have never studied Boolean algebra before, these symbols may be a little confusing. A full discussion of Boolean algebra will take us off on too much of a tangent, but it’s basically a special kind of algebra that’s used heavily in computing.

The symbols you will need to know are the following:

∧– AND
∨– OR
¬ – NOT
⊕ – XOR, which basically means either, but not both.

Now we can plug in the numbers for our initialization vectors that we discussed in the Initialization vectors section:

F (89abcdef, fedcba98, 76543210) = (89abcdef AND fedcba98) OR (NOT-89abcdef AND 76543210)

We can complete this calculation with an online Boolean calculator. However, we will need to divide it into separate steps because this calculator doesn’t allow us to use parentheses to order the equation properly.

If you want to try it out for yourself:

Enter 89abcdef into input A.
Select AND from the dropdown menu below it.
Enter fedcba98 into input B.
Select Hex from the four different number systems. It’s located right below the Operation Result.

The answer appears next to Operation Result:

88888888

Now, let’s do the other half of the equation:

Select NOT to the left of input A.
Enter 89abcdef into input A.
Select AND from the dropdown menu below it.
Enter 76543210 into input B.
Select Hex from the four different number systems, located right below the Operation Result.

Our answer is:

76543210

We’ve solved part of the equation, so now we know that:

F(B, C, D) = 88888888 OR 76543210

We can finish it by:

Entering 88888888 into input A (make sure that the NOT box is no longer selected).
Selecting OR from the dropdown menu below it.
Entering 76543210 into input B.
Selecting Hex from the four different number systems, located right below the Operation Result.

If you’ve done it right, the output of F(B, C, D) should be:

fedcba98

Boolean algebra works differently to normal algebra. If you are confused by the whole process, you may have to do some background study at the Boolean algebra page we linked above. Otherwise, you’ll just have to trust us.

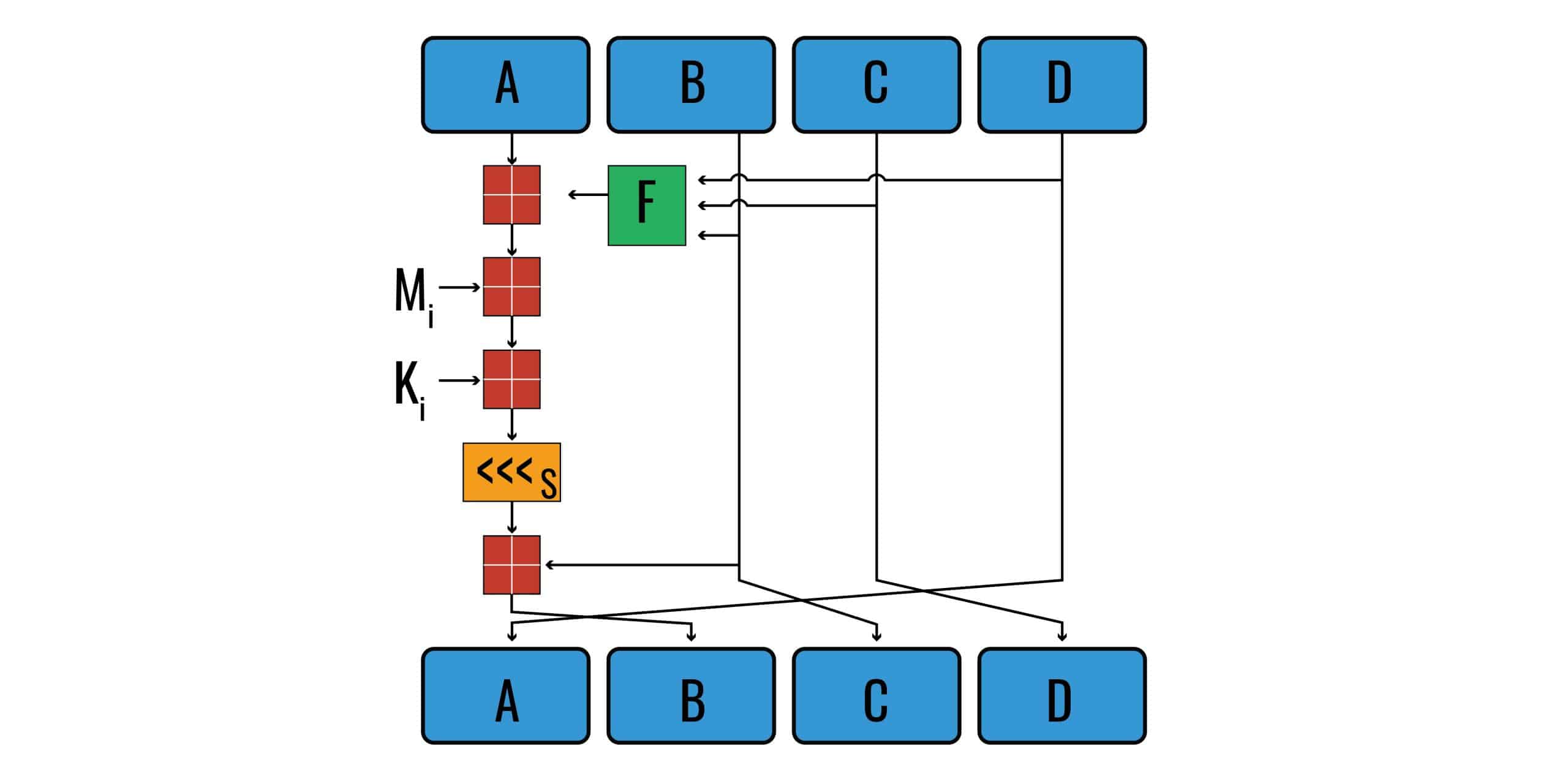
So far we’ve only completed our first calculation. Take a look at the diagram to see where we are heading:

All we’ve done is run values B, C and D through Function F. There’s a whole lot more to go just in this diagram. This diagram represents just one operation, and there are sixteen of them in a round. There are four rounds for each 512-bit block, giving us a total of 64 operations. If there is more than one 512-bit block of input data, each block has to undergo these 64 operations. We have a lot to get through, so let’s move along.

Modular addition

If you look at the arrow coming out of the F box, you will see that it points into another square that looks kind of like a window. There’s also an arrow from the A going into this box. The box symbol represents modular addition.

We introduced modular operations in our other article on MD5. You can revisit that section if you need a quick reminder. However, it may be more helpful to refer to the following article on modular arithmetic, because modular addition is a little different to the modular operations we talked about earlier.

The formula for this step of the algorithm is:

(X + Y) mod Z

Where:

X – 01234567 (the initialization vector A, a predefined value which we discussed in the The MD5 algorithm’s Initialization vectors section)

Y – fedcba98 (the result of function F from the previous step)

Z – 100000000 (this is the equivalent to 2³² (which ensures that the result of this equation are no more than eight characters long)

When we put everything into our formula, we get:

(01234567 + fedcba98) mod 100000000

We will use this online calculator to do the modulo operation. First, select hexadecimal for “Number a type”, “Number b type”, “Number c type” and “Convert calculation result to a”. Once more, we will have to split up the operation into parts, because this calculator doesn’t allow parentheses either.

Enter:

01234567 into “Number a value”.

fedcba98 into “Number b value”.

Type “add(a,b)” into the field where it says “Calculation equation”. This simply tells the calculator to add the numbers we have typed in for A and B. This gives us a result of:

ffffffff

For the next step, enter:

ffffffff into “Number a value”.

100000000 into “Number b value”.

mod(a,b) into “Calculation equation”.

If you have done everything right, when you click Calculate, you should get the following answer:

ffffffff

If you are still confused by how these calculations work, perhaps it’s a good idea to check out the modular arithmetic link posted above. Another option is to convert the hexadecimal numbers into decimal numbers. By converting the numbers into decimal and running through the calculations in a number system you are more familiar with, it might help you figure out what’s actually happening. You can then convert your answer back into hexadecimal to see if it’s the same.

The first portion of our message input

Now that we have our output from this first modular addition box, it’s time to move on. If you follow the line leaving the box, you will see that it points to another of the same modular addition boxes. To the left of this box, we see an arrow with Mi pointing toward it as well. These represent our two inputs in the next calculation.

If you remember what we discussed at the start of The input M section, each 512 block of input is divided up into sixteen 32-bit “words”, labelled M0-M15. The i in the diagram is a general placeholder for whichever word the algorithm is up to. In this case, we are just starting, so we are dealing with the first word, M0.

When we broke down our input into sixteen 32-bit words in The input M section, M0 was 54686579 in hexadecimal.

In addition to our M0 input, we also need our output from the last step, ffffffff. The box indicates that we need to perform modular addition with both of these numbers, just like in the previous section.

The formula for this step of the algorithm is also:

(X + Y) mod Z

Where:

X – 54686579 (M0)

Y – ffffffff (the output from the previous section)

Z – 100000000 (this is 2³²)

Therefore:

(54686579 + ffffffff) mod 100000000

We are going to use the same online calculator. This time, it’s the same equation, but with different inputs, so we’ll go through it much faster. If you get lost, just refer to the previous section and replace the values with these new inputs.

Enter:

54686579 into “Number a value”.

ffffffff into “Number b value”.

add(a,b) into “Calculation equation”.

Hit the Calculate button. It will give you an answer of:

154686578

Copy this value and insert it into “Number a value” field. Insert 100000000 into “Number b value”. Change the formula to mod (a,b). If you have done everything correctly, when you hit calculate, you should get an answer of:

54686578

With this output in hand, it’s time to move on to the next step.

Adding in the constant

Referring back to our diagram, when we follow the line out of the previous box, we see yet another one of the boxes that indicate modular addition. This time, we need our output from the last operation to act as an input, as well as what the diagram refers to as Ki.

K refers to a constant, of which there are 64 different ones, one for each of the operations involved in processing a 512-bit block. i is just a placeholder for whichever constant we are up to. Since this is still the first operation, we will use K1 first (the RFC does not state why the message input, M starts at M0, while the constant starts at 1). Each of the values for K are shown in the The operations section. If you refer back, you will see that K1 is:

d76aa478

Once more, our function is:

(X + Y) mod Z

Our values are:

X – d76aa478

Y – 54686578 (the output from the previous operation)

Z – 100000000 (2³²)

When we plug everything in, we get:

(d76aa478 + 54686578) mod 100000000

Using the same online calculator, we enter the following inputs:

d76aa478 into “Number a value”.

54686578 into “Number b value”.

add(a,b) into “Calculation equation”.

Hit the Calculate button. It will give you an answer of:

12bd309f0

Copy this value and insert it into “Number a value” field. Insert 100000000 into “Number b value”. Change the formula to mod (a,b). If you have done everything correctly, when you hit calculate, you should get an answer of:

2bd309f0

The above is our output for this step of the operation.

Left bit-shift

When we follow the arrows once more, we see a box with several symbols pointing to the left. This signifies that we need to take our input from the previous operation and shift it to the left. The number of spaces we shift depends on the round, according to the predefined values that we listed in the The operations section.

Since this is our first time going through the function, we start with S1. If you consult the listing, you will see that the value for S1 is 7. This means that we need to shift our value seven spaces to the left. As with everything that computers do, this happens at the binary level, and it will be easier for us to see what’s going on if we temporarily convert our hexadecimal number back into binary.

So let’s take the output from our previous step:

2bd309f0

And use an online converter to switch it to binary:

0010 1011 1101 0011 0000 1001 1111 0000

All we have to do is move each bit 7 spaces to the left. We will do it with an intermediate step to make it easier to see what is going on:

001 0101 1110 1001 1000 0100 1111 1000 0xxx xxxx

We have added in the seven x symbols at the right to represent the shift. However, this space is actually replaced by the seven leftmost numbers which we have underlined. The seven bit rotation really looks like this:

1110 1001 1000 0100 1111 1000 0001 0101

If we convert this number back to hexadecimal, we get:

e984f815

As you can see, while this left bit-shift seems like a relatively similar step, it makes the string look radically different to us.

More modular addition

Looking back at the diagram once more, when we trace the lines onward, we see that the result of our left shift goes to another modular addition box. The other input traces back to the B at the top, which is the initialization vector B. If you refer back to the The MD5 algorithm’s initialization vectors section, you will see that this value is 89abcdef.

By now, you should be pretty familiar with modular addition and the steps we have been taking to solve it. The formula is:

(X + Y) mod Z

This time:

X – 89abcdef (initialization vector B)

Y – e984f815 (the output from the previous section)

Z – 100000000 (2³²)

When we put all of the numbers in, we get:

(89abcdef + e984f895) mod 100000000

Let’s use our online calculator to enter:

89abcdef into “Number a value”.

e984f815 into “Number b value”.

add(a,b) into “Calculation equation”.

Click the Calculate button to get an answer of:

17330C604

Now it’s time to copy and insert this value into “Number a value” field. Type 100000000 into “Number b value” and change the formula to mod (a,b). This should give you an answer of:

7330C604

The end… of the first operation

We have basically finished the first operation. If you trace the arrow leaving the last modular addition box we worked on, it ends up pointing to the B at the bottom. These values at the bottom for A, B, C and D will act as the initialization vectors for the second operation.

This means that the output of the last step will become the initialization vector B for the next operation. It replaces the original initialization vector B, which was 89abcdef. If you follow all of the other lines, we end up with:

D as the new initialization vector for A.
The output of the entire operation as the initialization vector for B.
B as the new initialization vector for C.
C as the new initialization vector for D.

Only 63 more operations to go…

Summary of the first operation

Before we move ahead, it’s best to give a quick summary of the many complicated steps we have been through.

We started off with our four initialization vectors:

A – 01234567
B – 89abcdef
C – fedcba98
D – 76543210

We put these last three values through the F function:

F(B, C, D) = (B∧C)∨(¬B∧D)

This gave us a result of:

F(B, C, D) = fedcba98

We took this result and put it into the following formula for modular addition alongside the initialization vector A:

(X+Y) mod Z

Where:

X = 01234567

Y = fedcba98

Z = 100000000

This gave us an answer of:

ffffffff

Next, we did some more modular addition, this time with the first word of our initial input, M0, which is 54686579. We added it to the result of the last step with the same formula, which gave us:

54686578

The next step was some more modular addition, this time with a constant, K, which we listed the values for in the The operations section. K1 was d76aa478, which we added to the previous result, giving us an output of:

2bd309f0

The next step mixed things up, and we converted the hexadecimal result into binary, so that we could easily see the seven bit left-shift. When we changed it back to hexadecimal, the result was:

e984f815

We followed this by getting back to modular addition, adding this result to the initialization vector B, 89abcdef. We ended up with the following value, which becomes the initialization vector B in the next round:

7330c604

The values for B, C and D were also shuffled to the right, giving us new initialization vectors for the next operation:

A – 76543210
B – 7330c684
C – 89abcdef
D – fedcba98

The second operation

The second operation passes through the very same patterns as the previous operation, however, it is done with different values. Not only are the initialization vectors different, but so are some of the inputs. The operation proceeds along the following lines:

The new values for B, C and D are put through the F function in the same way as in the prior operation.
The result is then added to the new value for A through modular addition.
This time, the second word from the input message, M1 is added to the result from the prior step with modular addition. According to the The input M section, M1 is 54686579.
Modular arithmetic is used once more, this time adding the last outcome to the constant, which is K2. K2 is e8c7b756 according to our list of K values in the The operations section.
We then take the result from the last section and shift it to the left. However, instead of moving it seven spaces, this time we shift it twelve. This is because the values we laid out for the left bit-shifts in the The operations section stipulates that S2 is 12. This signals 12 moves to the left in the second operation.
This outcome is then added to the new value for initialization vector B with modular arithmetic.
The result becomes the new initialization vector B for the third operation. The values for B, C and D are also rotated to the right, so that B becomes the initialization vector C, C becomes the initialization vector D, and D becomes the initialization vector A.

Subsequent operations

By now, you have hopefully gotten the hang of what happens in each individual operation. Operations three through to 16 each begin with the results from the previous operations as the “initialization vectors”. However, these results have always been shifted one letter to the right.

Subsequent operations involve:

The values for B, C and D going through the F function.
The results being added to the respective A values through modular addition.
The results being added to the respective portion of the message input, Mi.
The results being added to the respective constant, Ki.
The results being shifted left a set number of spaces, according to the Si.
The results being added to initialization vector B and this value becoming the new initialization vector B in the next round.
The other three values being shifted one space to the right.

The final values from operation three become the initialization vectors for operation four, and the final values from operation four become the initialization vectors for operation five. This pattern continues until the 16th operation, which uses the results from the 15th round as its initialization vectors. The results of operation 16 will become “initialization vectors” for the first operation of round two.

Round two

Let’s zoom out for a minute and take a look at the overall structure of the algorithm. We’ve gone through the first lot of 16 operations, and now we are shifting onto the second round. The diagram doesn’t really do the algorithm justice and include everything, but if it did it would become too messy:

Right now, we have the outputs from round one, which will become our initialization vectors for the first operation of round two in the second long rectangle.

Things change at the start of round two. Its first operation, the 17th overall, begins with a different function. The F function is replaced by the G function, which will be used for operations 17 through 32. The G function is as follows:

G (B, C, D) = (B∧D)∨(C∧¬D)

The values for B, C and D are whatever the outputs from the previous operation were, just like before. For a refresher on Boolean algebra:

∧– AND
∨– OR
¬ – NOT

So the formula is basically saying, G (B, C, D) equals (B AND D) OR (C AND NOT D).

Figuring out the correct values for each of the previous 16 operations doesn’t sound very fun, so we will just make some up instead. It will still give you an idea of how this new G function works, and save you from scrolling through pages of repetition. Let’s say that the 16th operation led to the following initialization vectors for the 17th round:

A – 799d1352
B – 2c34dfa2
C – de1673be
D – 4b976282

Therefore:

G (B, C, D) = (2c34dfa2∧4b976282)∨(de1673be∧¬4b976282)

We will need to complete the calculation in steps, because this online calculator for logical expressions doesn’t allow parentheses for ordering the operations. Let’s start by finding the result of the first part:

(2c34dfa2∧4b976282)

Enter 2c34dfa2 into input A.
Select AND from the dropdown menu below it.
Enter 4b976282 into input B.
Select Hex from the four different number systems, located right below the Operation Result.

This gives us a result of:

8144282

Now, let’s take care of the other half of the equation:

(de1673be∧¬4b976282)

Switch out the old value for input A and place de1673be there instead.
You can leave the same 4b976282 value in input B, just click the NOT button to the left of it.

You should get the following as your result:

1400113c

Now that we have the results of both (B∧D) and (C∧¬D), we can do the OR operation.

8144282 ∨ 1400113c

We need to:

Enter 8144282 into input A.
Select OR from the dropdown menu below it.
Enter 1400113c into input B. Make sure that NOT is no longer selected.
Select Hex from the four different number systems, located right below the Operation Result.

This gives us a result for G (B, C, D) of:

1c1453be

This value then gets sent into the modular addition function along with the initialization vector we made up for A. Everything else proceeds pretty much the same as during the operations we described above, with the outputs from the previous operation becoming inputs into the next round. Each operation uses its respective Mi and Ki inputs, as well as the Si shifts we specified in the The operations section.

Round three

Once the 32nd operation has been completed, its outputs are used as initialization vectors for the 33rd operation. However, because this is the start of the third round, the H function is used from now until the end of the 48th operation. The formula is:

H (B, C, D) = B⊕C⊕D

The H function is also a function of (B, C and D). The ⊕ symbol on the right side of the equation may be unfamiliar to you. It’s generally known as an XOR operation, short for exclusive or. In practical terms its output is true (in the logical sense) if one of its input arguments is true, but not if both of them are.

Let’s make up some outputs from the 32nd round to act as initialization vectors for this function in the 33rd round:

A – eb160cd0
B – d5071367
C – c058ade2
D – 63c603d7

This gives us:

H(B, C, D) = d5071367 ⊕ c058ade2 ⊕ 63c603d7

Let’s go back to our online calculator and input this equation by:

Entering d5071367 into input A.
Selecting XOR from the dropdown menu below it.
Entering c058ade2 into input B.
Selecting XOR from the dropdown menu below it.
Entering 63c603d7 into input C.
Selecting Hex from the four different number systems, located right below the Operation Result.

This gives us a result for the H (B, C, D) function of:

7699bd52

Everything else continues as above, except with their respective input values for each operation.

Round four

When we get to the 49th operation, it’s time for the beginning of the fourth round. We get a new formula, which we will use up until the end of the 64th round:

I(B, C, D) = C⊕(B∨¬D)

This formula also has the XOR function for one or the other, but not both. It’s basically saying “C OR, BUT NOT BOTH (B OR NOT-D). Let’s make up some more outputs from the end of the 48th round:

A – 60cdceb1
B – 7d502063
C – 8b3d715d
D – 1de3a739

Therefore:

I(B, C, D) = 8b3d715d⊕(7d502063∨¬1de3a739)

Let’s do the bracketed part of the operation in our online calculator first. Enter it by:

Placing 7d502063 into input A.
Selecting OR from the dropdown menu below it.
Entering 1de3a739 into input B.
Selecting clicking NOT beside input B.
Selecting Hex from the four different number systems, located right below the Operation Result.

This gives us an output of:

7f5c78e7

The rest of the equation is therefore:

8b3d715d ⊕ 7f5c78e7

To finish it:

Place 8b3d715d into input A.
Select XOR from the dropdown menu below it.
Enter the result of our last calculation, 7f5c78Ee7, into input B (make sure that the NOT beside it is no longer selected).
Select Hex from the four different number systems, located right below the Operation Result.

This gives us an output of:

f46109ba

The rest of this operation continues in the same way that each of the operations that came before did. This result is added to initialization vector A with modular arithmetic, and each of the other steps are followed with the respective input values for this round. Ultimately, this gives us outputs which are used as the initialization vectors for operation 50, which also uses function I.

This process continues up until (and including) the 64th round.

The final step of the MD5 algorithm, after 64 operations

The 64th operation proceeds like each of those before it, using the outputs of the 63rd operation as its initialization vectors for the I function. When it has gone through each of the steps of the operation, it gives us new values for A, B, C and D.

Let’s say that these values are:

A – 60cdceb1
B – 7d502063
C – 8b3d715d
D – 1de3a739

First, we’ll zoom out again and take a look at the larger MD5 algorithm:

By this stage, we have finished the bottom rectangle that says “16 operations of…”. If you follow the arrows down, you will see that they are connected to a box with four modular addition calculations. The other inputs come from the initialization vectors that we used at the very start of the MD5 algorithm.

For this stage, let’s refer to them as OIV-A, OIV-B, etc. for original initialization vector A, B, etc.. This should help to keep things clear. These original initialization vectors were:

OIV-A – 01234567
OIV-B – 89abcdef
OIV-C – fedcba98
OIV-D – 76543210

Once again, our equation for modular addition is:

(X + Y) mod Z

In this case:

X – 60cdceb1 (The output for initialization vector A after the 64th operation).
Y – 01234567 (OIV-A).
Z – 100000000 (this is 232).

Therefore:

(60cdceb1 + 01234567) mod 100000000

Let’s return to our online calculator for modular addition. Once again, we will have to do this equation in stages, because the calculator doesn’t allow parentheses. Let’s add the first two numbers by entering:

60cdceb1 into “Number a value”.
01234567 into “Number b value”.

Put “add(a,b)” into “Calculation equation”. Make sure that you have Hexadecimal selected for “Number a type”, “Number b type” and “Convert calculation result to a”.

Click the Calculate button to get an answer of:

61f11418

Now it’s time to copy and insert this value into “Number a value” field. Type 100000000 into “Number b value” and change the formula to “mod (a,b).” This should give you an answer of:

61f11418

This is the answer for the final value of A (in the case of a single 512-bit block of input data).

The last three calculations of the MD5 algorithm

We need to do the exact same equation for our remaining numbers:

(A + B) mod C

Therefore, we need to solve:

(B + OIV-B) mod C
(C + OIV-C) mod C
(D + OIV-D) mod C

When we plug in the respective numbers, we get:

(7d502063 + 89abcdef) mod 100000000
(8b3d715d + fedcba98) mod 100000000
(1de3a739 + 76543210) mod 100000000

By now, you should be pretty familiar with how each of these equations work, so you should be able to compute them on your own if you want to. If you want to skip the hard work, the answers are:

B – 06fbee52 (the calculator will actually give you an answer of 6fbee52. We have simply added the zero at the front to bring it up to eight characters in length)
C – 8a1a2bf5
D – 9437d949

The hash of an MD5 hash function

Because we are only computing the hash for a single 512-bit block of data, we have all of the information we need for the final hash. It’s simply a concatenation (this is just a fancy word that means we put the numbers together) of these latest values for A, B, C and D:

Hash = ABCD

Therefore, the hash of our original message of “They are deterministic” is:

H (They are deterministic) = 61f1141806fbee528a1a2bf59437d949

Larger message inputs

If the initial input was 448 bits or larger, it would need to be split into two or more 512-bit blocks. In the first block, the input would be added essentially the same way we have described throughout. The only difference comes in the final step.

After operation 64, the results for A, B, C and D are added to OIV-A, OIV-B, OIV-C and OIV-D using modular addition, as above. However, these results would not be concatenated to form the final hash.

Instead, the result of A + OIV-A would act as the initialization vector A for the beginning of the second 512-bit block of data. The results of B + OIV-B, C + OIV-C and D + OIV-D would form the initialization vectors for B, C and D, respectively, in this second 512-bit block of data.

The second 512 bits of input would be divided up into sixteen 32-bit words, just as the initial 512 bits of data were. Each of these new words would become M0, M1, M2 …M15 for the MD5 algorithm to run again. All of the other variables would be the same as in the previous steps.

There would be four rounds of 16 operations each, for a total of 64 operations. Each round would have its own function, functions F, G, H and I, which would be used in the same order and in the same way as last time.

If the initial input was only two 512-bit blocks long, the last parts of the MD5 hash algorithm would proceed in essentially the same way as they did in the The final step, after 64 operations section, finally outputting the hash for the two 512-bit blocks of input data.

If the initial input was more than two 512-bit blocks long, the A, B,C and D outputs that would have otherwise formed the hash are instead used as initialization vectors for the third block.

This process would continue until all of the initial input has been processed, no matter how many 512-bit blocks it takes. Whenever it comes to the last block, the algorithm would follow the process outlined in the The final step, after 64 operations section, ultimately delivering us new values for A, B, C and D. These would then be concatenated to form the hash.