What is RSA Encryption

RSA encryption is a system that solves what was once one of the biggest problems in cryptography: how can you send someone a coded message without having an opportunity to previously share the code with them?

This article will teach you everything you need to know about how RSA encryption was developed, how it works, the math behind it, what it is used for as well as some of the biggest security issues that it faces. Learning about RSA will give you some foundational knowledge that helps you to understand how many parts of our online life are kept secure.

What is RSA encryption?

Let’s say you want to tell your friend a secret. If you’re right next to them, you can just whisper it. If you are on opposite sides of the country, that obviously won’t work. You could write it down and mail it to them, or use the phone, but each of these communication channels is insecure and anyone with a strong enough motivation could easily intercept the message.

If the secret was important enough, you wouldn’t risk writing it down as spies or a rogue postal employee could be looking through your mail. Likewise, someone could be tapping your phone without your knowledge and logging every single call you make.

One solution to prevent eavesdroppers from accessing message contents is to encrypt it. This basically means to add a code to the message which changes it into a jumbled mess. If your code is sufficiently complex, then the only people who will be able to access the original message are those who have access to the code.

If you had a chance to share the code with your friend beforehand, then either of you can send an encrypted message at any time, knowing that you two are the only ones with the ability to read the message contents. But what if you didn’t have a chance to share the code beforehand?

This is one of the fundamental problems of cryptography, which has been addressed by public-key encryption schemes (also known as asymmetric encryption) like RSA.

Under RSA encryption, messages are encrypted with a code called a public key, which can be shared openly. Due to some distinct mathematical properties of the RSA algorithm, once a message has been encrypted with the public key, it can only be decrypted by another key, known as the private key. Each RSA user has a key pair consisting of their public and private keys. As the name suggests, the private key must be kept secret.

Public key encryption schemes differ from symmetric-key encryption, where both the encryption and decryption process use the same private key. These differences make public key encryption like RSA useful for communicating in situations where there has been no opportunity to safely distribute keys beforehand.

Symmetric-key algorithms have their own applications, such as encrypting data for personal use, or for when there are secure channels that the private keys can be shared over.

See also: Public key cryptography

Where is RSA encryption used?

RSA encryption is often used in combination with other encryption schemes, or for digital signatures which can prove the authenticity and integrity of a message. It isn’t generally used to encrypt entire messages or files, because it is less efficient and more resource-heavy than symmetric-key encryption.

To make things more efficient, a file will generally be encrypted with a symmetric-key algorithm, and then the symmetric key will be encrypted with RSA encryption. Under this process, only an entity that has access to the RSA private key will be able to decrypt the symmetric key.

Without being able to access the symmetric key, the original file can’t be decrypted. This method can be used to keep messages and files secure, without taking too long or consuming too many computational resources.

RSA encryption can be used in a number of different systems. It can be implemented in OpenSSL, wolfCrypt, cryptlib and a number of other cryptographic libraries.

As one of the first widely used public-key encryption schemes, RSA laid the foundations for much of our secure communications. It was traditionally used in TLS and was also the original algorithm used in PGP encryption. RSA is still seen in a range of web browsers, email, VPNs, chat and other communication channels.

RSA is also often used to make secure connections between VPN clients and VPN servers. Under protocols like OpenVPN, TLS handshakes can use the RSA algorithm to exchange keys and establish a secure channel.

The background of RSA encryption

As we mentioned at the start of this article, before public-key encryption, it was a challenge to communicate securely if there hadn’t been a chance to safely exchange keys beforehand.

If there wasn’t an opportunity to share the code ahead of time, or a secure channel through which the keys could be distributed, there was no way to communicate without the threat of enemies being able to intercept and access the message contents.

It wasn’t until the 1970s that things really began to change. The first major development towards what we now call public-key cryptography was published at the start of the decade by James H. Ellis. Ellis couldn’t find a way to implement his work, but it was expanded upon by his colleague Clifford Cocks to become what we now know as RSA encryption.

The final piece of the puzzle is what we now call the Diffie-Hellman key exchange. Malcolm J. Williamson, another co-worker, figured out a scheme that allowed two parties to share an encryption key, even if the channel was being monitored by adversaries.

All of this work was undertaken at the UK intelligence agency, the Government Communications Headquarters (GCHQ), which kept the discovery classified. Partly due to technological limitations, the GCHQ couldn’t see a use for public-key cryptography at the time, so the development sat idly on the shelf gathering dust. It wasn’t until 1997 that the work was declassified and the original inventors of RSA were acknowledged.

Several years later, similar concepts were beginning to develop in the public sphere. Ralph Merkle created an early form of public-key cryptography, which influenced Whitfield Diffie and Martin Hellman in the design of the Diffie-Hellman key exchange.

Diffie and Hellman’s ideas were missing one important aspect that would make their work a foundation of public key cryptography. This was a one-way function that would be difficult to invert. In 1977, Ron Rivest, Adi Shamir and Leonard Adleman, whose last names form the RSA acronym, came up with a solution after a year of laboring on the problem.

The MIT-based academics made their breakthrough after a Passover party in 1977. After a night of drinking, Rivest went home, but instead of sleeping, he spent the evening feverishly writing a paper that formalized his idea for the necessary one-way function.

The idea was patented in 1983 by MIT, but it wasn’t until the early days of the internet that the RSA algorithm began to see widespread adoption as an important security tool.

How does RSA encryption work?

The following is going to be a bit of a simplification, because too many readers have probably been scarred by their high school math teacher. To keep the math from getting too out-of-hand, we will be simplifying some concepts and using much smaller numbers. In reality, RSA encryption uses prime numbers that are much larger in magnitude and there are a few other complexities.

There are several different concepts you will have to get your head around before we can explain how it all fits together. These include trapdoor functions, generating primes, Carmichael’s totient function and the separate processes involved in computing the public and private keys used in the encryption and decryption processes.

Trap door functions

RSA encryption works under the premise that the algorithm is easy to compute in one direction, but almost impossible in reverse. As an example, if you were told that 701,111 is a product of two prime numbers, would you be able to figure out what those two numbers are?

Even with a calculator or a computer, most of us wouldn’t have any idea of where to start, let alone be able to figure out the answer. But if we flip things around, it becomes much easier. What’s the result of:

907 x 773

If you were bored enough, you would have been able to whip out your phone or maybe calculate it in your head to discover that the answer is the previously mentioned 701,111. This 907 and 773 are the prime numbers that answer our first question, which shows us that certain equations can be easy to figure out one way, but seemingly impossible in reverse.

Another interesting aspect of this equation is that it is simple to figure out one of the prime numbers if you already have the other one, as well as the product. If you are told that 701,111 is the result of 907 multiplied by another prime number, you can figure it out the other prime with the following equation:

701,111 ÷ 907 = 773

Since the relationship between these numbers is simple to compute in one direction, but incredibly hard in reverse, the equation is known as a trap door function. Be aware that while the above example is hard for people to figure out, computers can do the operation in a trivial amount of time.

Because of this, RSA uses much larger numbers. The size of the primes in a real RSA implementation varies, but in 2048-bit RSA, they would come together to make keys that are 617 digits long. To help you visualize it, a key would be a number of this size:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

Generating primes

The trap door functions mentioned above form the basis for how public and private-key encryption schemes work. Their properties allow public keys to be shared without endangering the message or revealing the private key. They also allow data to be encrypted with one key in a way that can only be decrypted by the other key from the pair.

The first step of encrypting a message with RSA is to generate the keys. To do this, we need two prime numbers (p and q) which are selected with a primality test. A primality test is an algorithm that efficiently finds prime numbers, such as the Rabin-Miller primality test.

The prime numbers in RSA need to be very large, and also relatively far apart. Numbers that are small or closer together are much easier to crack. Despite this, our example will use smaller numbers to make things easier to follow and compute.

Let’s say that the primality test gives us the prime numbers that we used above, 907 and 773. The next step is to discover the modulus (n), using the following formula:

n = p x q

Where p = 907 and q = 773

Therefore:

n = 907 x 773

n = 701,111

Carmichael’s totient function

Once we have n, we use Carmichael’s totient function:

    λ(n) = lcm (p − 1, q − 1)

If it’s been a while since you’ve hit the math textbooks, the above might look a bit terrifying. You can skip over this part and just trust that the math works, otherwise stick with us for a few more calculations. Everything will be explained in as much detail as possible to help you get your head around the basics.

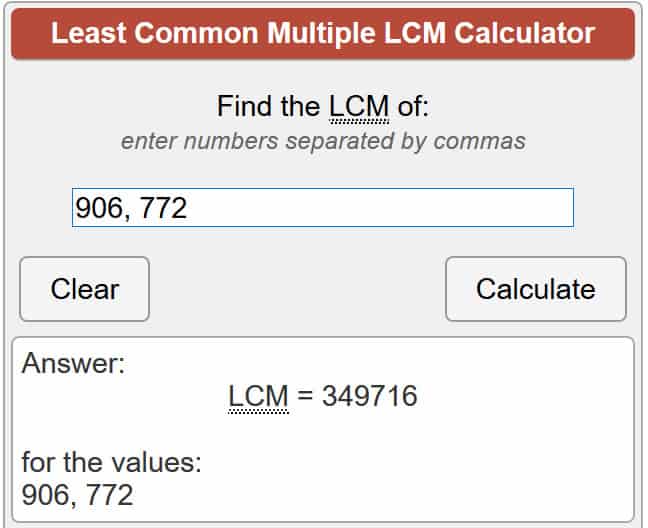
For those who aren’t aware, λ(n) represents Carmichael’s totient for n, while lcm means the lowest common multiple, which is the lowest number that both p and q can divide into. There are a few different ways to figure this out, but the easiest is to trust an online calculator to do the equation for you. So let’s put our numbers into the equation:

    λ(701,111) = lcm (907 − 1, 773 − 1)

    λ(701,111) = lcm (906, 772)

   Using the calculator linked above, this gives us:

rsa-encryption-2

    λ(701,111) = 349,716

Generating the public key

Now that we have Carmichael’s totient of our prime numbers, it’s time to figure out our public key. Under RSA, public keys are made up of a prime number e, as well as modulus n (we will explain what modulus means in a few paragraphs). The number e can be anything between 1 and the value for λ(n), which in our example is 349,716.

Because the public key is shared openly, it’s not so important for e to be a random number. In practice, e is generally set at 65,537, because when much larger numbers are chosen randomly, it makes encryption much less efficient. For today’s example, we will keep the numbers small to make calculations efficient. Let’s say:

e = 11

Our final encrypted data is called the ciphertext (c). We derive it from our plaintext message (m), by applying the public key with the following formula:

c = me mod n

As we mentioned, e mod n is the public key. We have already devised e and we know n as well. The only thing we need to explain is mod. It’s a little bit out of the depth of this article, but it refers to a modulo operation, which essentially means the remainder left over when you divide one side by the other. For example:

10 mod 3 = 1

This is because 3 goes into 10 three times, with a remainder of 1.

Back to our equation. To keep things simple, let’s say that the message (m) that we want to encrypt and keep secret is just a single number, 4. Let’s plug everything in:

c = me mod n

c = 411 mod 701,111

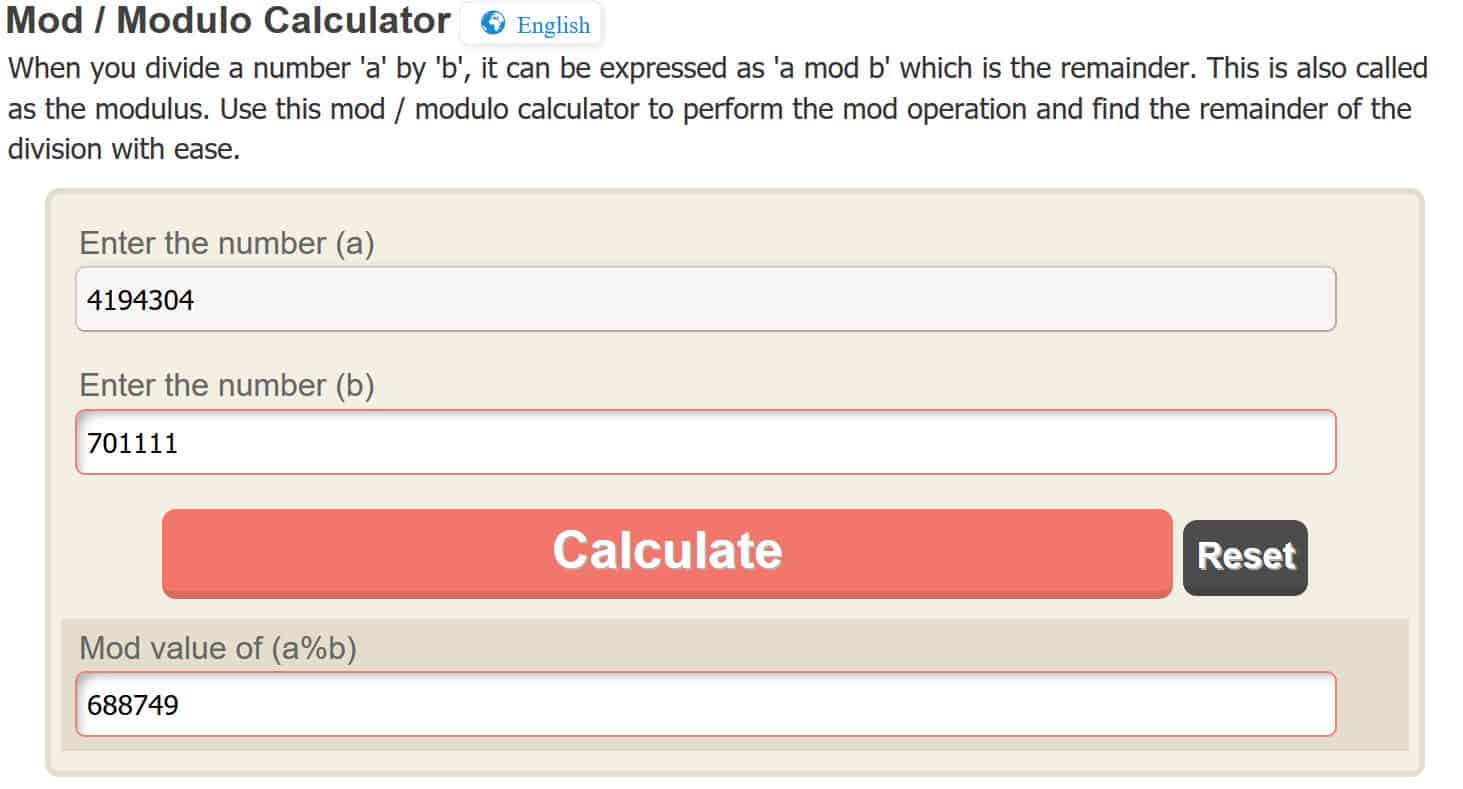
c = 4,194,304 mod 701,111

Again, to make the modulo operation easy, we will be using an online calculator, but you are welcome to figure it out for yourself. By entering 4,194,304 into the online calculator, it gives us:

rsa-encryption-3

c = 688,749

Therefore when we use RSA to encrypt our message, 4, with our public key, it gives us the ciphertext of 688,749. The previous steps may have seemed a little too math-heavy, but it’s important to reiterate what has actually happened.

We had a message of 4, which we wanted to keep secret. We applied a public key to it, which gave us the encrypted result of 688,749. Now that it is encrypted, we can securely send the number 688,749 to the owner of the key pair. They are the only person who will be able to decrypt it with their private key. When they decrypt it, they will see the message that we were really sending, 4.

Generating the private key

In RSA encryption, once data or a message has been turned into ciphertext with a public key, it can only be decrypted by the private key from the same key pair. Private keys are comprised of d and n. We already know n, and the following equation is used to find d:

d =1/e mod λ(n)

In the “Generating the public key” section above, we already decided that in our example, e would equal 11. Similarly, we know that λ(n) equals 349,716 from our earlier work under Carmichael’s totient function. Things get a little more complicated when we come across this section of the formula:

1/e mod

This equation may look like it is asking you to divide 1 by 11, but that’s not the case. Instead, this just symbolizes that we need to calculate the modular inverse of e (which in this case is 11) and λ(n) (which in this case is 349,716).

This essentially means that instead of performing a standard modulo operation, we will be using the inverse instead. This is normally found with the Extended Euclidean Algorithm, but it’s a little outside of the scope of this article, so we will just cheat and use an online calculator instead. Now that we understand everything that’s going on, let’s plug our information into the formula:

d =1/11 mod 349,716

To perform this operation, simply input 11 (or any value you may have for e if you are attempting this with your own example) where it says Integer and 349,716 (or any value you may have for λ(n) if you are attempting this with your own example) where it says Modulo in the online calculator that was linked above. If you have done it correctly, you should get a result where:

d = 254, 339

Now that we have the value for d, we can decrypt messages that were encrypted with our public key using the following formula:

m = cd mod n

We can now go back to the ciphertext that we encrypted under the “Generating the private key” section. When we encrypted the message with the public key, it gave us a value for c of 688,749. From above, we know that d equals 254,339. We also know that n equals 701,111. This gives us:

m = 688,749254,339 mod 701,111.

As you may have noticed, trying to take a number to the 254,339th power might be a little bit much for most normal calculators. Instead, we will be using an online RSA decryption calculator. If you wanted to do use another method, you would apply the powers as you normally would and perform the modulus operation in the same way as we did in the “Generating the public key” section.

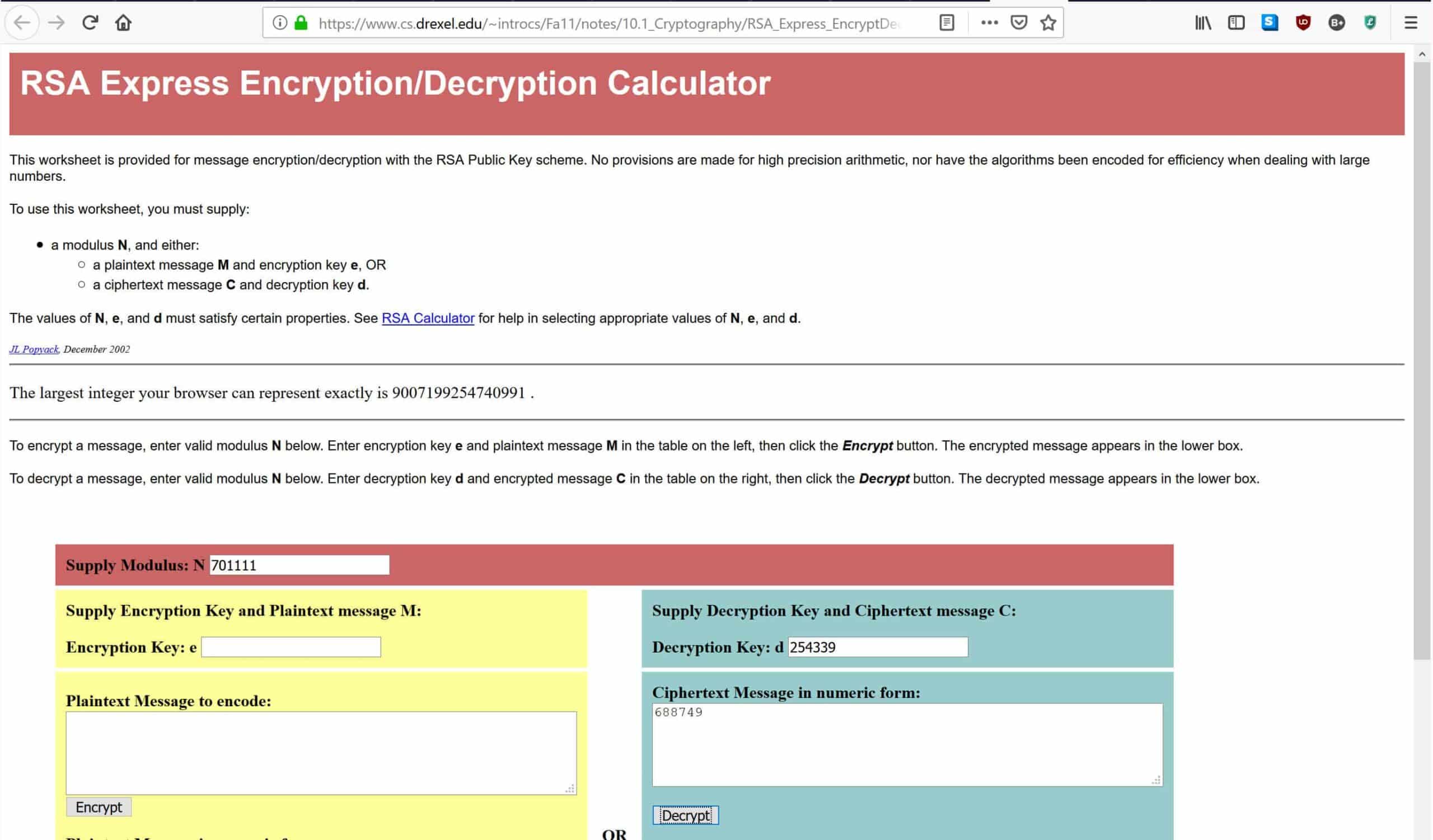
In the calculator linked above, enter 701,111 where it says Supply Modulus: N, 254,399 where it says Decryption Key: D, and 688,749 where it says Ciphertext Message in numeric form, as shown below:

rsa-encryption-1

Once you have entered the data, hit Decrypt, which will put the numbers through the decryption formula that was listed above. This will give you the original message in the box below. If you have done everything correctly, you should get an answer of 4, which was the original message that we encrypted with our public key.

How RSA encryption works in practice

The above sections should give you a reasonable grasp of how the math behind public key encryption works. It can be a little confusing, but even those who didn’t understand the intricacies of the equations can hopefully take away some important information about the process.

In the steps listed above, we have shown how two entities can securely communicate without having previously shared a code beforehand. First, they each need to set up their own key pairs and share the public key with one another. The two entities need to keep their private keys secret in order for their communications to remain secure.

Once the sender has the public key of their recipient, they can use it to encrypt the data that they want to keep secure. Once it has been encrypted with a public key, it can only be decrypted by the private key from the same key pair. Even the same public key can’t be used to decrypt the data. This is due to the properties of trap door functions that we mentioned above.

When the recipient receives the encrypted message, they use their private key to access the data. If the recipient wants to return communications in a secure way, they can then encrypt their message with the public key of the party they are communicating with. Again, once it has been encrypted with the public key, the only way that the information can be accessed is through the matching private key.

In this way, RSA encryption can be used by previously unknown parties to securely send data between themselves. Significant parts of the communication channels that we use in our online lives were built up from this foundation.

How are more complicated messages encrypted with RSA?

In our example, we simplified things a lot to make it easier to understand, which is why we only encrypted a message of “4”. Being able to encrypt the number 4 doesn’t seem particularly useful, so you might be wondering how you can encrypt a more complicated set of data, such as a symmetric key (which is the most common use of RSA), or even a message.

Some people may be perplexed at how a key like “n38cb29fkbjh138g7fqijnf3kaj84f8b9f…” or a message like “buy me a sandwich” can be encrypted by an algorithm like RSA, which deals with numbers and not letters. The reality is that all of the information that our computers process is stored in binary (1s and 0s) and we use encoding standards like ASCII or Unicode to represent them in ways that humans can understand (letters).

This means that keys like “n38cb29fkbjh138g7fqijnf3kaj84f8b9f…” and messages like “buy me a sandwich” already exist as numbers, which can easily be computed in the RSA algorithm. The numbers that they are represented by are much larger and harder for us to manage, which is why we prefer to deal with alphanumeric characters rather than a jumble of binary.

If you wanted to encrypt a longer session key or a more complex message with RSA, it would simply involve a much larger number.

Padding

When RSA is implemented, it uses something called padding to help prevent a number of attacks. To explain how this works, we’ll start with an example. Let’s say you were sending a coded message to a friend:

Dear Karen,

    I hope you are well. Are we still having dinner tomorrow?

    Yours sincerely,

    James

Let’s say that you coded the message in a simple way, by changing each letter to the one that follows it in the alphabet. This would change the message to:

Efbs Lbsfo,

    J ipqf zpv bsf xfmm. Bsf xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    Kbnft

If your enemies intercepted this letter, there is a trick that they could use to try and crack the code. They could look at the format of your letter and try to guess what the message might be saying. They know that people normally begin their letters with “Hi”, “Hello”, “Dear” or a number of other conventions.

If they tried to apply “Hi” or “Hello” as the first word, they would see that it wouldn’t fit the number of characters. They could then try “Dear”. It fits, but that doesn’t necessarily mean anything. The attackers would just try it and see where it led them. So they would change the letters “e”, “f”, “b”, and “s” with “d”, “e”, “a”, and “r” respectively. This would give them:

Dear Laseo,

    J ipqe zpv are xemm. Are xe tujmm iawjoh djooes upnpsspx?

    Zpvrt tjoderemz,

    Kanet

It still looks pretty confusing, so the attackers might try looking at some other conventions, like how we conclude our letters. People often add “From” or “Kind regards” at the end, but neither of these fit the format. Instead, the attackers might try “Yours sincerely” and replace the other letters to see where it gets them. By changing “z”, “p”, “v”, “t”, “j” “o”, “d” and “m” with “y”, “o”, “u”, “s”, “i”, “n”, “c” and “l” respectively, they would get:

Dear Lasen,

    I ioqe you are xell. Are xe tuill iawinh dinnes uonossox?

    Yours sincerely,

    Kanet

After that modification, it looks like the attackers are starting to get somewhere. They have found the words “I”, “you” and “are”, in addition to the words that made up their initial guesses.

Seeing as the words are in correct grammatical order, the attackers can be pretty confident that they are heading in the right direction. By now, they have probably also realized that the code involved each letter being changed to the one that follows it in the alphabet. Once they realize this, it makes it easy to translate the rest and read the original message.

The above example was just a simple code, but as you can see, the structure of a message can give attackers clues about its content. Sure, it was difficult to figure out the message from just its structure and it took some educated guesswork, but you need to keep in mind that computers are much better at doing this than we are. This means that they can be used to figure out far more complex codes in a much shorter time, based on clues that come from the structure and other elements.

If the structure can lead to a code being cracked and reveal the contents of a message, then we need some way to hide the structure in order to keep the message secure. This brings us to padding.

When a message is padded, randomized data is added to hide the original formatting clues that could lead to an encrypted message being broken. With RSA, things are a little bit more complicated, because an encrypted key doesn’t have the obvious formatting of a letter that helped to give us clues in our above example.

Despite this, adversaries can use a number of attacks to exploit the mathematical properties of a code and break encrypted data. Due to this threat, implementations of RSA use padding schemes like OAEP to embed extra data into the message. Adding this padding before the message is encrypted makes RSA much more secure.

Signing messages

RSA can be used for more than just encrypting data. Its properties also make it a useful system for confirming that a message has been sent by the entity who claims to have sent it, as well as proving that a message hasn’t been altered or tampered with.

When someone wants to prove the authenticity of their message, they can compute a hash (a function that takes data of an arbitrary size and turns it into a fixed-length value) of the plaintext, then sign it. They sign the hash by applying the same formula that is used in decryption (m = cd mod n). Once the message has been signed, they send this digital signature to the recipient alongside the message.

If a recipient receives a message with a digital signature, they can use the signature to check whether the message was authentically signed by the private key of the person who claims to have sent it. They can also see whether the message has been changed by attackers after it was sent.

To check the digital signature, the recipient first uses the same hash function to find the hash value of the message they received. The recipient then applies the sender’s public key to the digital signature, using the encryption formula (c = me mod n), to give them the hash of the digital signature.

By comparing the hash of the message that was received alongside the hash from the encrypted digital signature, the recipient can tell whether the message is authentic. If the two values are the same, the message has not been changed since it was signed by the original sender. If the message had been altered by even a single character, the hash value would be completely different.

RSA security & attacks

Like most cryptosystems, the security of RSA depends on how it is implemented and used. One important factor is the size of the key. The larger the number of bits in a key (essentially how long the key is), the more difficult it is to crack through attacks such as brute-forcing and factoring.

Since asymmetric-key algorithms such as RSA can be broken by integer factorization, while symmetric-key algorithms like AES cannot, RSA keys need to be much longer to achieve the same level of security.

Currently, the largest key size that has been factored is 829 bits long. This was achieved in 2020 by an international team of computer scientists using tens of thousands of machines over the course of a few months.

As computing power is still increasing, it can be assumed that future attempts of similar intensity will be able to factor much larger RSA keys.

Despite this, the time and resources needed for this kind of attack puts it out of the reach of most hackers and into the realm of nation states. The best key length to use will depend on your individual threat model. The National Institute of Standards and Technology recommends a minimum key size of 2048-bit, but 4096-bit keys are also used in some situations where the threat level is higher.

Factoring is just one way that RSA can be broken. A number of other attacks have the potential to break the encryption with a smaller amount of resources, but these depend on the implementation and other factors, not necessarily RSA itself. Some of these include:

Are the primes really random?

Some implementations of RSA use weak random number generators to come up with the primes. If these numbers aren’t sufficiently random, it makes it much easier for attackers to factor them and break the encryption. This problem can be avoided by using a cryptographically secure pseudo-random number generator.

Poor key generation

RSA keys need to fall within certain parameters in order for them to be secure. If the primes p and q are too close together, the key can easily be discovered. Likewise, the number d that makes up part of the private key cannot be too small. A low value makes it easy to solve. It’s important that these numbers are of adequate length to keep your key safe.

Side channel attacks

These are a type of attack that don’t break RSA directly, but instead use information from its implementation to give attackers hints about the encryption process. These attacks can include things like analyzing the amount of power that is being used, or branch prediction analysis, which uses execution-time measurements to discover the private key.

Another type of side channel attack is known as a timing attack. If an attacker has the ability to measure the decryption time on their target’s computer for a number of different encrypted messages, this information can make it possible for the attacker to ascertain the target’s private key.

Most implementations of RSA avoid this attack by adding a one-off value during the encryption process, which removes this correlation. This process is called cryptographic blinding.

Is RSA encryption safe for the future?

The good news is that RSA is currently considered safe to use, despite these possible attacks. The caveat is that it needs to be implemented correctly and use a key that falls within the correct parameters. As we have just discussed, implementations that don’t use padding, use inadequately sized primes or have other vulnerabilities can not be considered safe.

If you want to use RSA encryption, make sure that you are using a key of at least 1024 bits. Those with higher threat models should stick to keys of 2048 or 4096 bits if they want to use RSA with confidence.

As long as you are conscious of the weaknesses that RSA has and use it correctly, you should feel safe to use RSA for key sharing and other similar tasks that require public key encryption.

While RSA is safe for now, the rise of quantum computing is expected to pose some challenges in the future.

Will quantum computing affect RSA?

The field of quantum computing continues to make steady improvements, but it will still be some years before it sees much use outside of a research context. While quantum computers have immense potential for advancing our capabilities, they will also bring some complications to the world of cryptography.

This is because quantum computers may be able to easily solve certain problems that are currently considered immensely difficult, and this difficulty is often what makes our cryptographic systems secure. In the case of symmetric-key algorithms like AES, powerful quantum computers running Grover’s algorithm would be able to significantly speed up attacks.

While this certainly represents a threat against our current cryptographic mechanisms, it is also relatively easy to fix. All we will have to do is double the key size to protect these symmetric-key algorithms.

When it comes to public-key cryptography like RSA, we are presented with a much greater problem. Once quantum computers become strong enough that they can effectively run Shor’s algorithm, it will be feasible to solve the following three mathematical problems:

This is bad news, because the security of our most commonly used public-key algorithms relies on the premise that these are currently impractical to solve with current computational resources. In RSA’s case, it’s the integer factorization problem.

While quantum computing and Shor’s algorithm are certainly a future threat to RSA, the good news is that we have time to change our cryptographic infrastructure to ensure our future security.

Although it’s hard to know when exactly it will be feasible for quantum computers to break RSA, significant research and development in the area is already yielding results.

The US National Institute of Standards and Technology (NIST) is, after a seven-year slog, in the process of standardizing three encryption algorithms able to resist attack by quantum computers, with the fourth set for release in 2025. These quantum-resistant algorithms were selected from the 69 put forward by cryptographers back in 2017.

See also: Common encryption types explained