SHA-2 is a family of cryptographic hash functions that play a key part in keeping our data safe online. We’ve discussed its application in detail elsewhere. In this article we’ll focus on explaining in detail how the SHA-2 algorithm works.
What does SHA-2 do?
You might have a pretty good idea of why we use SHA-2 and what it does in a big picture sense. But what’s actually happening when we zoom in? How can we take a sentence like “hashing is complicated”, put it through an online SHA-256 calculator, and end up with a hash like this:
d6320decc80c83e4c17915ee5de8587bb8118258759b2453fce812d47d3df56a
How does a simple letter “A” give us something as equally complex?
559aead08264d5795d3909718cdd05abd49572e84fe55590eef31a88a08fdffd
How can the entire Declaration of Independence result in something so similar to a single letter, but also with such widely different values?
639505bee7bdae68f224b0d5bcb1c324d0e33011d2302839b7bedfab4515a1bb
What really goes on inside the SHA-2 algorithm?
How does the SHA-2 algorithm work?
We will investigate how the SHA-2 algorithm works through an example, going through each step that takes our message, “hashing is complicated”, and somehow gives us the convoluted output of:
d6320decc80c83e4c17915ee5de8587bb8118258759b2453fce812d47d3df56a
We will be demonstrating SHA-256 because it’s the most commonly used iteration. SHA-224, SHA-384, SHA-512, SHA-512/224 and SHA-512/256 all work in a similar manner, except that the two former algorithms have a block size of 512 bits, while the latter four have a 1024-bit block size. Note that SHA-384, SHA-512, SHA-512/224 and SHA-512/256 also include 80 rounds, rather than the 64 we will be describing.
They also use some slightly different input numbers at various points of the algorithm. SHA-512/224 and SHA-512/256 are truncated versions of SHA-512, meaning that the final hash is just the left-most 224 or 256 bits, respectively. You can refer to FIPS 180-4 for the specifics.
Converting to binary
When we enter “hashing is complicated” into an SHA-256 hash function, the first thing that happens is that the data is converted to binary. To simplify the explanation, this is essentially because humans and machines speak, understand and work in separate languages.
While it’s easy for us to think in words, computers do it all in zeros and ones. Whenever we use them, they are converting our letters and words into the binary language that they understand so that they can run calculations. However, all of this is generally done without us noticing, giving us a smooth user experience.
We convert letters, numbers and symbols into binary using the American Standard Code for Information Interchange (ASCII), which is basically just a system that a committee of smart people agreed on for translating between the two languages.
If we turn to an ASCII table, we can see that the first letter of our phrase, a lower case “h”, is written as “01101000” in binary. According to the same table, a lower case “a” is “01100001”, while an “s” is “01110011” and an “h” is “01101000”.
The letter “i” is “01101001”, while “n” is “01101110” and “g” is “01100111”. The binary code for a space is listed in the table at the top of the second column as the ASCII character “SP”, in the same row as the decimal number 32. It’s “00100000”.
Rather than running through every single letter of our example phrase, we will just enter it into an ASCII to binary converter. Typing it in gives us:
01101000 01100001 01110011 01101000 01101001 01101110 01100111 00100000 01101001 01110011 00100000 01100011 01101111 01101101 01110000 01101100 01101001 01100011 01100001 01110100 01100101 01100100
The above makes zero sense to us as humans, but to machines, it says, “hashing is complicated”.
SHA-2 and padding
Once we have rewritten our phrase in binary, the next step is to add padding, which is essentially a bunch of extra data that we add to our input to make it a fixed length. It also helps to prevent length extension attacks.
The different versions of SHA-2 have the following block sizes:
- SHA-224 – 512 bits
- SHA-256 – 512 bits
- SHA-384 – 1024 bits
- SHA-512 – 1024 bits
- SHA-512/224 – 1024 bits
- SHA-512/256 – 1024 bits
These block sizes are the amount of data that the SHA-2 algorithm processes in one go. We have shown that hash functions are capable of processing inputs as long as the Declaration of Independence (SHA-256 can actually take inputs that are orders of magnitude larger, at up to 264-1, which is such a huge number that you don’t really have to worry about the algorithm’s upper limits). However, it does not process this information all in one go.
Instead, in the case of SHA-256, it processes the information in 512-bit blocks of data. In our example, things are relatively straightforward, because our input “hashing is complicated” is less than 512 bits of data–it’s 176 bits. You can calculate it by counting each binary digit, or by counting each letter plus the two spaces, and then multiplying by 8, because each character is one byte in length.
However, we often need to hash inputs that are far greater than 512 bits in length. In these cases, the message is simply divided into blocks. If we needed to hash a 10,000-bit message, it would simply need to be split across multiple 512-bit blocks.
In our example, we only have 176 bits of data, but need to fill up a 512-bit block. This means that we will need to add 336 bits of padding to complete it. SHA-2 uses the following padding scheme:
- A “one” is added after the binary message data that is being hashed.
- Then, zeros are added until the length of the input data plus the additional one from the previous step add up to 448 bits. In our example, we have an input length of 176 bits, plus the one from the previous step, bringing us up to 177 bits. Therefore, we need 448 minus 177 zeros. If we do the math, we have to add 271 zeros.
- The final 64 bits of the final block (512 bits minus the 448 bits that we have already filled up in the prior steps) are set aside to display the length of the message in binary. As we are only dealing with one block of data, the end of it needs to include this 64-bit message length. Our message length in bits is 176, which is 10110000 in binary. This will go at the very end of the block, and the preceding numbers are filled up with more zeros (in cases where we have a much larger input, these zeros will be replaced by the longer message length written in binary).
If we put it all together, we end up with the following padded 512-bit block for the message “hashing is complicated”:
01101000 01100001 01110011 01101000 01101001 01101110 01100111 00100000 01101001 01110011 00100000 01100011 01101111 01101101 01110000 01101100 01101001 01100011 01100001 01110100 01100101 01100100 10000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 10110000
If you count out the ones and zeros, you will see that there are 512 bits of data in the above block. The first 176 bits are the input message in binary, “hashing is complicated”.
This is followed by the 1, which we have bolded and underlined to make it easier to see. Then we have the 271 zeros, followed by the 64-bit message length, which is also bolded and underlined. This message length is preceded by zeros, as we mentioned earlier.
In SHA-384, SHA-512, SHA-512/224 and SHA-512/256, the padding scheme is essentially the same, except that the blocks each need to be filled with 1024 bits of data and the final block has the following differences:
- In the second step, zeros are added until a length of 896 bits is reached, rather than 448 bits.
- In the final step, 128 bits of the block are set aside for appending the message length.
If we were running through our example with SHA-384, SHA-512, SHA-512/224 or SHA-512/256, the padded block would look much the same, except that it would have an extra 448 zeros from the second step, and another 64 zeros from the final step.
Inputs greater than 448 bits (for SHA-224 and SHA-256) and 896 bits (for SHA-384, SHA-512, SHA-512/224 and SHA-512/256)
We often need to hash message inputs that are greater than the block sizes of either 512 bits or 1024 bits, which means that we need to split the data across multiple blocks. The cut-off point for splitting blocks is actually either 447 bits or 895 bits, because at least one bit of padding, plus the 64-bit or the 128-bit message length must be included.
This means that if you have exactly 448 bits (or 896 bits) of data that you need to hash, it will have to be split across two blocks. The first block will include the entirety of the data, plus 64 (or 128) bits of padding (the one followed by 63 or 127 zeros). The second block will have another 448 (or 896) zeros, with the 64-bit (or 128-bit) message length tagged on at the end in the same way that we showed in the previous section.
449 bits (or 897 bits) of data would also take up two blocks of data, and would instead have a one plus 62 (or 126) zeros of padding before the message length.
On the other hand, 447 bits (or 895 bits) of data would just manage to fit in a single block. It would include the 447 (or 895) bits, then padding of a single one, followed by the message length of either 64 or 128 bits.
The system works the same for larger data inputs. The data is split across as many blocks as it takes in order for all of the data to be included, plus at least one digit of padding and with the 64-bit message length appended at the end of the final block.
In the case of 5,000 bits of input data and the 512-bit block sizes of SHA-224 or SHA-256, the input would be split across 10 blocks. The first nine would only include the input data, while the tenth would include the final 392 bits of input data, a one, 55 zeros and then the 64-bit message length at the end. This totals 5,120 bits of data, which is 10 multiplied by 512.
When using SHA-384, SHA-512, SHA-512/224 or SHA-512/256, those same 5,000 bits of data would be split across six 1024-bit blocks. The first four would only include the input data. The fifth block would include the final 904 bits of data, a one, and then 119 zeros as padding.
The 5,000 bits of data doesn’t quite fit within five blocks because the final 904 bits of data exceed the cut-off for the last block, which is 896 bits. The sixth block would include 896 zeros and then the 128-bit message length at the end.
The main SHA-2 algorithm
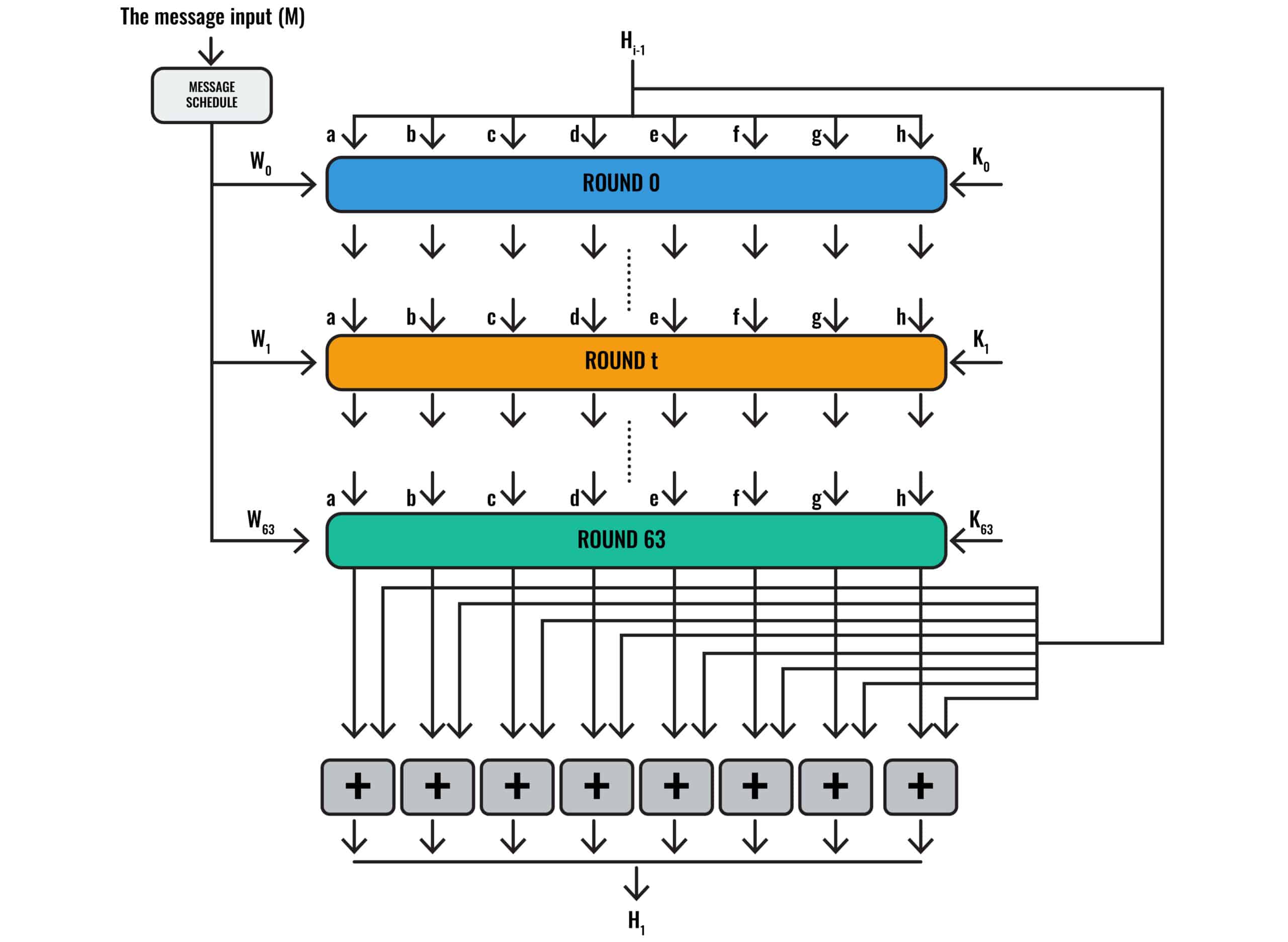
Below, we have a graphical representation of the SHA-2 algorithm:
The SHA-2 algorithm
Unless you’ve dealt with similar algorithms before, it probably doesn’t make a whole lot of sense. Don’t worry, because we’re going to spend a lot of time explaining it in detail.
The first thing that’s worth noting is that the diagram shows Round 0, Round T, and Round 63. Round 0 is the first round, while Round T is essentially a placeholder that represents any round in between, because it would be unwieldy to draw dozens of rounds. Round 63 is the final round, which gives us a total of 64 rounds if we are starting from 0.
Note that SHA-384, SHA-512, SHA-512/224 and SHA-512/256 involve 80 rounds instead of 64, so the process we are about to describe is somewhat different in these versions of the SHA-2 algorithm.
Each of these rounds features its own inputs and calculations, with the outputs of some calculations becoming inputs for subsequent ones. As you are probably beginning to figure out, the SHA-2 algorithm is complicated and involves a whole bunch of steps and computations.
The message input M
We will keep things simple in this example by only using our single 512-bit block of input, instead of a longer and more complicated input that requires a series of blocks. If we were to describe the process for longer data inputs, we would need to completely repeat much of the long, convoluted process we are about to lay out, with each one of the different blocks of input data.
If you look at the top left of the diagram above, you will see “The message input (M)”. This is the 512-bit padded block of our message “hashing is complicated”:
01101000 01100001 01110011 01101000 01101001 01101110 01100111 00100000 01101001 01110011 00100000 01100011 01101111 01101101 01110000 01101100 01101001 01100011 01100001 01110100 01100101 01100100 10000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 10110000
Our message input is first split up into sixteen 32-bit words labelled W0 to W15:
- W0 – 01101000 01100001 01110011 01101000
- W1 – 01101001 01101110 01100111 00100000
- W2 – 01101001 01110011 00100000 01100011
- W3 – 01101111 01101101 01110000 01101100
- W4 – 01101001 01100011 01100001 01110100
- W5 – 01100101 01100100 10000000 00000000
- W6 – 00000000 00000000 00000000 00000000
- W7 – 00000000 00000000 00000000 00000000
- W8 – 00000000 00000000 00000000 00000000
- W9 – 00000000 00000000 00000000 00000000
- W10 – 00000000 00000000 00000000 00000000
- W11 – 00000000 00000000 00000000 00000000
- W12 – 00000000 00000000 00000000 00000000
- W13 – 00000000 00000000 00000000 00000000
- W14 – 00000000 00000000 00000000 00000000
- W15 – 00000000 00000000 00000000 10110000
Converting to hexadecimal
Before we go any further, we will convert the above binary digits to another numbering system called hexadecimal. If you’ve been paying close attention, you may have noticed that our hash includes a bunch of letters:
d6320decc80c83e4c17915ee5de8587bb8118258759b2453fce812d47d3df56a
This is because hashes are generally written in hexadecimal, which is simply a different way to count, much in the same way that binary and the decimal system we are all accustomed to are different.
Binary is a base-2 system, which basically means you have two options, a 1 and a 0, before you have to start representing information with a greater number of digits.
Our regular decimal system is base-10, which means we have 10 options, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, before we run out and have to start combining numbers to represent larger amounts of data, such as when we combine a 1 and a 0 to make 10.
Hexadecimal is a base-16 system, which means we have 16 options:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a , b , c, d, e, f
When we use base-16, the value of 10 isn’t the same comfortable value we have grown up with. Instead, a 10 in base-16 is really the number 16 that we are accustomed to in decimal. In base-10, our familiar, decimal number 10 is represented with an a, 11 is b, 12 is c, 13 is d, 14 is e and 15 is f.
Going into too much depth on hexadecimal will distract from the main topic at hand, but you can find some more information here.
All you need to know is that we are switching our input from binary to hexadecimal, and we will do so by entering our binary values into a simple online converter (if you are trying this yourself and copying the binary numbers from above, remove the spaces). It should give you:
- W0 – 68617368
- W1 – 346E6720
- W2 – 69732063
- W3 – 6F6D706C
- W4 – 69636174
- W5 – 65648000
- W6 – 00000000
- W7 – 00000000
- W8 – 00000000
- W9 – 00000000
- W10 – 00000000
- W11 – 00000000
- W12 – 00000000
- W13 – 00000000
- W14 – 00000000
- W15 – 000000B0
Message schedule: Finding the other W values
The SHA-2 algorithm
If you scrutinize the diagram closely, you will notice that one of the inputs for Round 63 is W63. We only have W0 to W15 so far, so this implies that we need another 48 values before we have all of our W inputs.
In the SHA-384, SHA-512, SHA-512/224 and SHA-512/256 versions of the algorithm, we would need 80 values in total, so we would need to derive an extra 64.
These inputs are calculated in the box marked message schedule in the diagram. In both cases, we derive them using the following formula:
W t = σ1 (Wt-2) + Wt-7 + σ0 (Wt-15) + Wt-16
Confused? Don’t blame us, blame the cryptographers who designed it. Let’s start by trying to explain a couple of the values in the equation above.
t is essentially a stand-in for whichever round we are up to. If we are in the first round, which the engineers graciously call Round 0, t is 0. So if you see W0, it means the value for W in Round 0. We use this notation, because we will be using a large number of different values for W at various stages of the algorithm. Many of the other variables also use changing values throughout the stages of the algorithm.
The next value you are probably confused about is:
σ1(x)
The symbol is known as a sigma, and alongside the number 1 it stands in for the following function:
σ1(x) = ROTR17(x)⊕ROTR19(x)⊕SHR10(x)
Before we can fully understand how the message schedule works, we will need to explain this function.
Shift operations
The ROTR from the prior equation signals that we need to perform a circular right-shift on the value that follows it, x. It is shifted according to the number of bits shown in superscript. Let’s take the first segment:
ROTR17(x)
The above is really just saying to shift the value x 17 bits to the right. To give you an example of how this works, if the value for x is 1000 1001 and we want to perform a circular right-shift of just 1 bit, we would essentially just take the value in the rightmost column:
1000 1001
And move it to the left:
1100 0100
To demonstrate the concept again, this time with a circular shift to the right of 3 bits, we take the same number:
1000 1001
This time, we take each of the three rightmost digits and move them to the left:
0011 0001
This type of operation is involved in both the first section of the equation, as well as the middle one, with shifts of 17 and 19 bits respectively.
The last portion of the equation says:
SHR10(x)
The SHR tells us to perform a similar, yet slightly different operation, known as a logical left-shift. In this case, we left-shift the value x by the number of bits in superscript, 10, and then pad out the right side with zeros. Let’s take the same number as before to demonstrate how this works:
1000 1001
We will perform a shift of 10 bits to the left in 10 steps, with the last digit bolded for no other reason than to help you keep track of its progress:
0001 0010
0010 0100
0100 1000
1001 0000
0010 0000
0100 0000
1000 0000
0000 0000
0000 0000
0000 0000
Over the first seven moves, we saw the data slowly moving across to the left and being replaced with zeros on the right. By the eighth move, all of the original data was completely gone and had been replaced by zeros.
Note the difference between this logical left-shift operation and the previously discussed circular right-shift. Not only does the movement occur in different directions, but the circular right-shift recycles the data to the other side, while the logical left-shift discards it and fills the space that opens up with zeros
Discussing these shifts in too much detail will take us off on a tangent, but you can find out more about how they work at this resource.
XOR operations
The final part of our operation we need to explain is the ⊕ symbol, which links each of these components together. ⊕ stands for XOR operation, which is a logical operation that basically means its output is true if either input is true, but is false if both inputs, or neither input, are true.
It’s hard to explain this without delving into a full lecture on Boolean algebra and logical operations. This link gives you a bit of a rundown, but you don’t really need to understand it in depth to get a decent overview of how the rest of the algorithm functions. All you have to know is that we will basically be adding some numbers together, but using some weird math that you probably didn’t learn in school.
Solving the first part of our equation
Now that we’ve covered some of the details of the operations, let’s take another look at the equation we got stumped on:
W t = σ1 (Wt-2) + Wt-7 + σ0 (Wt-15) + Wt-16
Where:
σ1(x) = ROTR17(x)⊕ROTR19(x)⊕SHR10(x)
And:
σ0(x) = ROTR7(x)⊕ROTR18(x)⊕SHR3(x)
Now, let’s try to figure out the value for W16, because it’s the first number we need to figure out using this equation. Let’s plug in our value:
W16 = σ1 (W16-2) + W16-7 + σ0 (W16-15) + W16-16
Therefore:
W16 = σ1 (W14) + W9 + σ0 (W1) + W0
We know all of the W values on the right-hand side of the equation because they are the W words we figured out by splitting up our padded message block. The values in both binary and hexadecimal are:
- W0 – 68617368 or 01101000 01100001 01110011 01101000
- W1 – 346E6720 or 0110100 01101110 01100111 00100000
- W9 – 00000000 or 00000000 00000000 00000000 00000000
- W14 – 00000000 or 00000000 00000000 00000000 00000000
Before we plug all of the numbers in, let’s figure out what the value is for σ1 (W14), using the equation we discussed above:
σ1 (W14) = ROTR17(W14)⊕ROTR19(W14)⊕SHR10(W14)
With the W14 values in hexadecimal, the equation looks like:
σ1 (00000000) = ROTR17(00000000)⊕ROTR19(00000000)⊕SHR10(00000000)
The first step is to do the shifts that we described earlier for each section of the equation. We will switch to the binary value for W14 rather than the hexadecimal one, because it makes it easier to see the shifts we will be performing. Note that the binary and hexadecimal versions are simply different representations of the very same value, so switching them when it’s convenient doesn’t cause any problems:
ROTR17(00000000 00000000 00000000 00000000)
The outcome of the above operation will be extremely predictable because it’s all zeros, but we will run through it anyway, just to give you an idea of what’s going on. Head to the following online tool and enter the binary value for W14, the 32 zeros, into the input field marked Value. Make sure to remove the spaces. Enter 32 in Size, because the input value is 32 bits long. Type 17 in the Shift field, to make sure it shifts the value 17 spaces. Make sure that the direction is set to Right. Select the Circular Shift box and then click Perform bit shift operation. This performs the circular right-shift.
Unsurprisingly, this will give you a value of:
00000000 00000000 00000000 00000000
It looks like nothing happened, but the zeros were moved around. We just can’t tell and it seems meaningless, because they are all zeros.
Now, it’s time to perform the middle section of the operation:
ROTR19(00000000 00000000 00000000 00000000)
In this case, everything is the same, except the Shift value is now 19. This gives us an output of:
00000000 00000000 00000000 00000000
Now for the final part:
SHR10(00000000 00000000 00000000 00000000)
Remember, the SHR represents a logical left-shift, so this time, we need to tweak the settings. The Value and Size remain the same, but we need to make sure that:
Shift is set to 10
Direction is set to Left
Logical shift is selected.
Again, we get the same output of:
00000000 00000000 00000000 00000000
While this may have seemed like a pointless endeavor, it was only because our starting number was all zeros. When you perform these operations with other numbers, changes will actually occur.
Binary and hexadecimal strings of zero are the same, so we will switch these values back to hexadecimal when we move on to the next part of our calculation, so that it fits on the page better:
σ1 (W14) = 00000000 ⊕ 00000000 ⊕00000000
We can solve this equation in this online calculator by entering:
00000000 into field A.
Selecting XOR from the dropdown menu beneath it.
00000000 into field B.
Selecting XOR from the dropdown menu beneath it.
00000000 into field C.
If you’ve done it right, it should show A XOR B XOR C in the box marked Logical expression. It will give you the answer in the box marked Operation Result. In this case, it’s:
0 or 00000000 or 00000000 00000000 00000000 00000000.
It’s a boring answer, but it takes us one step closer to solving our equation, because now we know that:
σ1 (W14) = 00000000
If you scroll back, you will see that we just need to find one more component, and then we will be able to solve the equation. We need to find the value for σ0 (W1), which uses the following equation:
σ0(x) = ROTR7(x)⊕ROTR18(x)⊕SHR3(x)
As we stated above, we know that W1 is :
346E6720
Therefore:
σ0(346E6720) = ROTR7(346E6720)⊕ROTR18(346E6720)⊕SHR3(346E6720)
This equation is almost exactly the same as the one we just solved. For the sake of brevity, we won’t go into it, but if you would like to have a go yourself, just follow each of the steps we followed above, but change the Shift each time to 7, 18 and 3, respectively.
σ0(346E6720) = 4068DCCE ⊕ 99C80D1B ⊕ A3733901
Once you have solved it, you will find that the answer is:
σ0(346E6720) = 7AD3E8D4
Modular addition
Now that we know the values for both σ1 (W14) and σ0 (W1), we are finally ready to figure out the value for W16:
W16 = σ1 (W14) + W9 + σ0 (W1) + W0
W16 = 00000000 + 00000000 + 7AD3E8D4 + 68617368
The above equation looks relatively straightforward. The only thing that we need to note is that the plus signs in it represent modular addition, rather than normal addition.
To demonstrate the concept with an 8-digit decimal number, if we were using modular addition to add 1 to 99,999,999, the answer isn’t 100,000,000 as you would expect. Instead, it simply rolls back to the start in the same way that 1 follows 12 on a clock. The answer is 0 or 00,000,000. Check out this primer if you need a brief introduction to modular arithmetic.
In essence, modular addition allows you to add numbers without your answer ever getting longer. Take the following as another decimal example:
76,487,639 + 98,094,034
Under normal addition, the answer would be:
76,487,639 + 98,094,034 = 174,581,673
With modular addition, we can simply throw away the 1, and our answer is:
76,487,639 + 98,094,034 = 74,581,673
We can do the very same calculations with the hexadecimal numbers in our equation:
W16 = 00000000 + 00000000 + 7AD3E8D4 + 68617368
We will solve it using this online calculator. In our example, we don’t need to bother adding the zeros because they won’t change the value, and we can simply add 7AD3E8D4 and 68617368. If you need to use the same tool to add more numbers in the future, you can simply perform the operation multiple times, adding the next number to the result from the previous equation.
We can solve our equation by typing 7AD3E8D4 into the online calculator’s first box and 68617368 into the second. This gives us a result of:
W16 = e3355c3c
Remember, this is supposed to be modular addition, so if the result had exceeded eight digits, we would need to remove the left-most digit. Our result is only 8 digits long, so we don’t have to worry in this instance.
It’s been a long and convoluted process, but we finally have the answer for W16. It’s e3355c3c. The same set of calculations need to be performed for all of the W values, from W17 to W63.
We’ve demonstrated how these calculations work, so it’s time to move on to the other aspects of the SHA-2 algorithm.
The initialization variables
Now that we have discussed where all of the W inputs come from, let’s return to our diagram:
The SHA-2 algorithm
At the top, you will notice that it says Hi-1. This represents the working variables, which act as inputs in each round. There are eight of these variables, and they are updated at the end of each round. To begin, the initialization variables, H(0) are:
- H(0)a = 6a09e667
- H(0)b = bb67ae85
- H(0)c = 3c6ef372
- H(0)d = a54ff53a
- H(0)e = 510e527f
- H(0)f = 9b05688c
- H(0)g = 1f83d9ab
- H(0)h = 5be0cd19
The above numbers are derived from the square roots of the first eight prime numbers, but where they come from doesn’t really matter for our purposes. All you have to know is that we need to begin with the specific numbers listed above.
In subsequent rounds, these values will be different. For both simplicity and to represent their changing values, the diagram displays these inputs as a, b, c, d, e, f, g, and h, rather than H(0)a, H(0)b, etc., or H(1)a, H(1)b, etc..
The constant, K
In each round, we take the working variables and combine them with the round-appropriate W value that we described in the prior section. If you look to the right side of the rounds in the diagram, you will see another input, K.
There are 64 separate 32-bit values for K, one for each of the 64 rounds. They are derived from the cube-roots of the first 64 prime numbers. In hexadecimal, these eight-character constants for each round are as follows, read from left to right before descending to the next row:
428a2f98 71374491 b5c0fbcf e9b5dba5
3956c25b 59f111f1 923f82a4 ab1c5ed5
d807aa98 12835b01 243185be 550c7dc3
72be5d74 80deb1fe 9bdc06a7 c19bf174
e49b69c1 efbe4786 0fc19dc6 240ca1cc
2de92c6f 4a7484aa 5cb0a9dc 76f988da
983e5152 a831c66d b00327c8 bf597fc7
c6e00bf3 d5a79147 06ca6351 14292967
27b70a85 2e1b2138 4d2c6dfc 53380d13
650a7354 766a0abb 81c2c92e 92722c85
a2bfe8a1 a81a664b c24b8b70 c76c51a3
d192e819 d6990624 f40e3585 106aa070
19a4c116 1e376c08 2748774c 34b0bcb5
391c0cb3 4ed8aa4a 5b9cca4f 682e6ff3
748f82ee 78a5636f 84c87814 8cc70208
90befffa a4506ceb bef9a3f7 c67178f2
Note that the values for K are 64 bits long in SHA-384, SHA-512, SHA-512/224 and SHA-512/256. There are also 80 of these values, rather than 64. You can check these out in FIPS 180-4 if needed.
The Maj operation
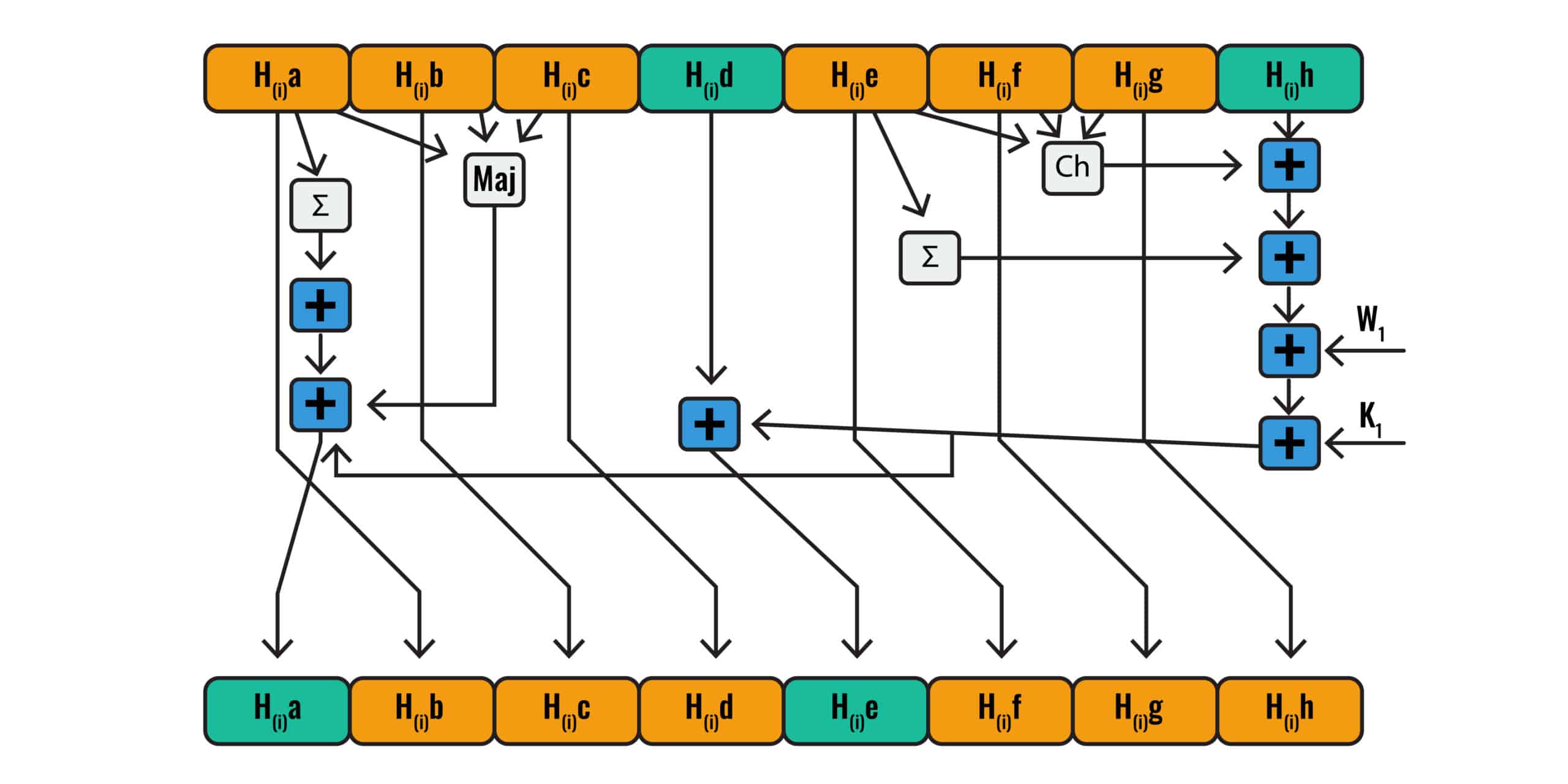
Finally, we have all of our inputs. Now it’s time to figure out how each round of SHA-2 uses them. The following diagram gives a good rundown of how SHA-2 uses all of these inputs:
The SHA-2 calculations involved in a single round.
If you look toward the top, we have the working variables, H(i)a, H(i)b, H(i)c, H(i)d, H(i)e, H(i)f, H(i)g, and H(i)h. These are the same as the working variables a, b, c, d, e, f, g, and h in the diagram for the whole SHA-2 algorithm. In the first round, they will be the respective initialization variables that we listed in the prior section. If you look at H(i)a, H(i)b, H(i)c, in the top left, you will see that all three inputs have arrows pointing to a box, Maj. This stands for the following equation:
Maj (a,b,c) = (a AND b) ⊕ (a AND c) ⊕ (b AND c)
To make the equation easier to read, we have taken out the H(i) from each variable and just left them as a, b, and c. As long as you remember that the values of a, b and c change with each round, this should make it easier to follow.
We have already dealt with the ⊕ symbol, but AND in this context is new to us. This is another operation in Boolean algebra. It refers to logical conjunction, which basically means the output is true only if both inputs are true. We’ll use an online calculator to perform this operation.
First, let’s throw in the initialization variables that we listed in the The initialization variables section:
Maj (6a09e667, bb67ae85, 3c6ef372) = (6a09e667 AND bb67ae85) ⊕ (6a09e667 AND 3c6ef372) ⊕ (bb67ae85 AND 3c6ef372)
The calculator we are using is fairly limited, so we will have to perform the calculation in several stages.
Enter 6a09e667 into input A.
Select AND from the drop down list below.
Enter bb67ae85 into input B.
This gives you a result of:
2A01A605
Next:
Enter 6a09e667 into input A.
Select AND from the drop down list below.
Enter 3c6ef372 into input B.
This gives you a result of:
2808E262
Then:
Enter bb67ae85 into input A.
Select AND from the drop down list below.
Enter 3c6ef372 into input B.
This gives you a result of:
3866A200
Let’s put all of these answers into the equation:
Maj (6a09e667, bb67ae85, 3c6ef372) = 2A01A605 ⊕ 2808E262 ⊕ 3866A200
Now, all we have to do is change the inputs in our online calculator one more time:
Enter 2A01A605 into input A.
Select XOR from the drop down list below.
Enter 2808E262 into input B.
Select XOR from the drop down list below.
Enter 3866A200 into input C.
This gives us:
Maj(a,b,c) = 3A6FE667
The ∑0 operation
Now that we have the answer for Maj(a,b,c) let’s refer back to the diagram and see what’s next:
The SHA-2 calculations involved in a single round.
You will see that the arrow from H(i)a also points to the ∑ symbol. This indicates that we need to take the H(i)a input and put it through the following computation:
∑0 (a) = ROTR2(a)⊕ROTR13(a)⊕ROTR22(a)
Once again, we have left out the H(i) for clarity. We have already dealt with these circular right-shifts, as well as the XOR operations. This time, we need to perform the circular right-shifts by 2, 13 and 22 bits, respectively. Let’s return to our calculator, with our value for a, 6a09e667.
For the first section of this calculation, enter:
6a09e667 into Value. Ensure hexadecimal is selected from the dropdown menu to the right.
32 into Size.
2 into Shift.
Make sure Right is selected for the Direction.
Click the Circular Shift box.
Click the Perform bit shift operation button.
This will give you a result of:
DA827999
If you want more insight into how this result was achieved, the calculator shows the steps involved in working out the operation. You can also refer back to the Shift operations section for further detail.
For the remaining two values we need to figure out, we only need to change the value in the Shift field and then click the Perform bit shift operation button again.
Changing it to 13 gives us an answer of:
333B504F
Changing it to 22 gives us an answer of:
27999DA8
We now have all of the values we need to finish the equation:
∑0 (6a09e667) = DA827999 ⊕ 333B504F ⊕ 27999DA8
Let’s return to the calculator we’ve been using for the XOR operations and:
Enter DA827999 into input A.
Select XOR from the drop down list below.
Enter 333B504F into input B.
Select XOR from the drop down list below.
Enter 27999DA8 into input C.
This gives us a result of:
∑0 (6a09e667) = CE20B47E
Modular addition of the results
If we follow the arrows from the Maj box and the ∑ box, we see that the outputs are then sent as inputs into a box with a + symbol on it. This represents modular addition, which as we already described, is much like normal addition, except the numbers simply roll over back to the start at a certain point, instead of continuing to grow larger. If you want a refresher with more detail, refer back to the prior modular addition section.
The diagram can be represented through the following formula:
Maj(a,b,c) + ∑0 (a) = 3A6FE667+ CE20B47E
We will be using a calculator again.
Enter 3A6FE667 into the first field and CE20B47E into the second, then click Calculate. This should give you an answer of:
108909ae5
If you are paying close attention, you may notice that the above answer is nine digits long, while each of the prior ones have only been eight. If you remember back to when we introduced the concept of modular addition, we mentioned that it’s like regular addition, but it just rolls over back to the start when the numbers get past a certain point.
Well, the calculator we have been using isn’t specifically for modular addition—it’s just performing the normal addition you learned in elementary school (but with hexadecimal numbers). This means that it won’t roll the numbers over once it reaches the limit. Up until this point, we’ve just been lucky that none of our previous calculations led to a nine-digit number.
This time we have ended up with nine digits, when we really need it to only be eight. The good news is that it’s easy to solve our problem. All we have to do is remove the leftmost digit, the 1. Therefore, our answer isn’t really 108909ae5. Instead, it’s:
08909ae5
If you return back to the diagram and trace the line that leaves this + box as an output, you will see that it connects up with another line that includes inputs that we have not dealt with yet. We will have to do some other calculations before we can return to this point.
The conditional function
This time, let’s look at H(i)e, H(i)f, H(i)g in the diagram. They all point to box labelled Ch, which indicates that these values act as inputs in the following function:
Ch(e, f, g) = (e AND f) ⊕ (NOT e AND g)
We have already dealt with each of these operations except for NOT. This represents negation, which is also known as the logical complement. We won’t go into the details of how it works to save us from going off on too much of a tangent, but you can either refer to the link or place your trust in the online calculator.
Once again, we have stripped away the H(i) from e, f and g, simply to make it easier to read. We are still working on Round 0, so these values will be the initialization variables that we listed earlier:
H(0)e – 510e527f
H(0)f – 9b05688c
H(0)g – 1f83d9ab
Note that in future rounds the variables for e, f and g will be different. For now, let’s put these initialization variables into our equation:
Ch (510e527f, 9b05688c, 1f83d9ab) = (510e527f AND 9b05688c) ⊕ (NOT 510e527f AND 1f83d9ab)
We will have to break this equation up into parts to complete it with our calculator. For the first half:
Enter 510e527f into input A.
Select AND from the drop down list below.
Enter 9b05688c into input B.
This should give you an answer of:
1104400C
For the second half of the equation:
Select the Not button to the left of input A.
Enter 510e527f into input A.
Select AND from the drop down list below.
Enter 1f83d9ab into input B.
This should give you a result of:
E818980
Let’s plug these answers back into the equation:
Ch(510e527f, 9b05688c, 1f83d9ab) = (1104400C) ⊕ (E818980)
Finish solving it by:
Making sure that NOT is no longer selected.
Enter 1104400C into input A.
Select XOR from the drop down list below.
Enter E818980 into input B.
This should give you an answer of:
Ch(e, f, g) = 1F85C98C
∑1: Circular right-shift
The SHA-2 calculations involved in a single round.
If you return to the diagram, you will see that H(i)e, isn’t only an input into the Ch equation that we just performed. It also becomes an input into another box marked with a ∑. This box signifies the following calculation:
∑1 (e) = ROTR6(e)⊕ROTR11(e)⊕ROTR25(e)
Note that this ∑1 (e) function is almost the same as the ∑0 (a) function that we performed in the The ∑0 operation section. However, the two have different values for the circular right-shifts.
We have left out the H(i) parts of the equation once again for simplicity’s sake. Let’s plug in the H(0)e value for the e values, because we are still working on Round 0. As we discussed in the The initialization variables section, the value for H(0)e is 510e527f. Therefore:
∑1 (510e527f) = ROTR6(510e527f)⊕ROTR11(510e527f)⊕ROTR25(510e527f)
We have explained how these right circular-shifts work several times, so let’s go to our online calculator and enter:
510e527f into Value. Ensure hexadecimal is selected from the dropdown menu to the right.
32 into Size.
6 into Shift.
Make sure Right is selected for the Direction.
Click the Circular Shift box.
Click the Perform bit shift operation button.
This should give us an answer of:
FD443949
Keep all of the details the same, except change the Shift value to 11 and click the Perform bit shift operation button once more. This should give you an answer of:
4FEA21CA
Repeat the process, this time just changing the Shift value to 25. Our answer should be:
87293FA8
Now we have each of the results we need to solve the equation. Let’s put each of the values we just figured out into the formula:
∑1 (510e527f) = FD443949⊕4FEA21CA⊕87293FA8
Now, let’s solve it by returning to our calculator for XOR operations:
Enter FD443949 into input A.
Select XOR from the drop down list below.
Enter 4FEA21CA into input B.
Select XOR from the drop down list below.
Enter 87293FA8 into input C.
This gives us a result of:
∑1 (510e527f) = 3587272B
Modular addition
Let’s head back to the diagram to see where to head next:
The SHA-2 calculations involved in a single round.
If we look at the top right, we will see that the working variable H(i)h has an arrow that leads to a box with a plus sign on it. The output from the Ch operation that we already completed leads to the same box, meaning that we need to perform modular addition with these two values. We are still in the middle of Round 0, so we need to use the initialization variable, H(0)h, as our value for h. As we discussed in the The initialization variable section.
H(0)h = 5be0cd19
The answer to the Ch operation was:
Ch(e, f, g) = 1F85C98C
Therefore we need to find the solution to:
5be0cd19 + 1F85C98C
Let’s head to our online calculator for hexadecimal addition.
Enter 5be0cd19 into the first field, and 1F85C98C into the second field, then click calculate. This gives us a result of:
7b6696a5
More modular addition
If you trace the arrow pointing out of this box with the + symbol, you will see that it becomes an input into another similar box, indicating more modular addition. This time, the other input is the result we got from performing the circular right shits on ∑1 (e) in the last ∑1: Circular right-shift section. The answer was:
∑1 (510e527f) = 3587272B
So let’s take the result from the last section and add it to the result of ∑1 (e). The equation is:
7b6696a5 + 3587272B
Go to the online calculator that we just used in the previous section, and enter 7b6696a5 into the first field, and 3587272B into the second field, then click calculate. This gives us a result of:
b0edbdd0
Adding the W value… with even more modular addition
If you consult the diagram again, you will see that the output from the prior operation goes into another of the modular addition boxes indicated by the + sign. This time, it gets added to one of the W values, which are portions of our padded message, “hashing is complicated” (in the case of values W16-W63, they are derived from the padded message, rather than being portions of it).
We are still in Round 0, so we need to use W0, which, as we discussed in the Converting to hexadecimal section toward the start, is:
W0 – 68617368
If we add this into a modular addition equation alongside the solution from our last section, we get:
68617368 + b0edbdd0
Return to the same online calculator for adding hexadecimal numbers and input 68617368 into the first field, then b0edbdd0 into the second one. Click Calculate, which will give you an answer of:
1194f3138
As we noted in the Modular addition of the results section, whenever one of our results reaches nine digits in length instead of eight, we need to roll it back by simply removing the leftmost digit, the 1. Therefore, the result we need isn’t actually 1194f3138. Instead, it’s:
194f3138
Adding the constant K… through the ever-reliable modular addition
With the above answer in hand, the output from the box points to another one that has the + symbol, indicating modular addition once more. This time, the other arrow that points toward it says Ki, which means that now it’s time to add the constant, K. We listed out each of the 64 values for K in The constant, K section. The value that we need for the first round, K0 is:
428a2f98
So our modular addition operation needs to include this value, plus the result from the prior round:
428a2f98 + 194f3138
Now, we need to return to our online calculator for hexadecimal addition and enter 428a2f98 into the first field, with 194f3138 in the second. Clicking calculate gives us a result of:
5bd960d0
The modular addition never ends
Return to the diagram and follow the output from the prior operation. It meets yet another dreaded modular addition box, this time with the value H(i)d as its other input. We are still in Round 0, so we need to use the initialization variable H(0)d, which is:
a54ff53a
Therefore we need to find the answer to:
a54ff53a + 5bd960d0
When we put these values into the same online calculator, we end up with:
10129560a
Once again, we have run into nine digits, so we simply need to drop the leftmost 1, as discussed in the Modular addition of the results section. Therefore, our answer is really:
0129560a
Where do the working variables come from?
If you follow the line out of the + symbol box, you will see that it ends up in a row of boxes at the bottom, with this particular box marked H(i)e. We have mentioned that Round 0 starts with initialization variables, but that the following rounds use different variables instead.
You may have wondered where these were going to come from, and now you have at least part of the answer. The values in this row of boxes at the bottom will become the working variables that are used in the next round.
In this case, the initialization variable H(0)d was added to what is essentially a mixture of the other initialization variables H(0)e, H(0)f, H(0)g, and H(0)h, alongside a portion of our input message, W0, and the constant, K0. The resulting mixture, 0129560a, then becomes the working variable H(1)e for Round 1.
The other initialization variables follow similar processes, being modified and added to each other in strange ways to become new working variables in the next round. You can look at the arrows pointing toward the bottom row to see where each of the next round’s working variables come from.
This may not seem that significant, but it’s a key component of the structure that allows each SHA-2 hash to look radically different, even when only a single letter of the input is changed. Remember, we are still only part of the way through Round 0, and there are 63 more rounds to go, so there is a lot more opportunity to mix up these values.
Uniting both sides… with more modular addition
Remember back to the Modular addition of the results section where we performed modular addition on the following values:
Maj(a,b,c) + ∑0 (a) = 08909ae5
After we found the solution, we had to pause on that thread of the diagram while we figured out the other components. Now, we’ve done everything we need to do and we are ready to go back to it.
Just to make sure you are following on okay, we are currently at the lowest + box on the left hand side of the diagram, which is fed into by the equation discussed above. Our other input in this modular addition equation is the solution from the The modular addition never ends section, which was:
0129560a
Therefore, we are trying to find the solution to:
08909ae5 + 0129560a
Let’s go back to our online calculator and type in 08909ae5 into the first field, with 0129560a in the second. When we hit calculate, it gives us:
9b9f0ef
We can add a zero to the front to keep it consistent at 8 digits:
09b9f0ef
This answer then gets placed in the H(i)a slot in the bottom row, which means that it will become the working variable H(1)a in the next round, Round 1.
Now that we have this solution, we have finally finished all of the many calculations involved in Round 0.
The other working variables
We already discussed the working variable H(i)e, and now the working variable H(i)a as well. Now it’s time to cover where the rest of the working variables come from so that we can use them in Round 1 and each of the subsequent rounds.
As we discussed, in Round 0, the working variables were a set of predefined numbers that we termed the initialization variables:
- H(0)a = 6a09e667
- H(0)b = bb67ae85
- H(0)c = 3c6ef372
- H(0)d = a54ff53a
- H(0)e = 510e527f
- H(0)f = 9b05688c
- H(0)g = 1f83d9ab
- H(0)h = 5be0cd19
Now it’s time to figure out what the rest of these working variables will be for the start of Round 1. Thankfully, the diagram makes it pretty easy:
The SHA-2 calculations involved in a single round.
If we look at the bottom row where it says H(i)b, we can trace back the arrow to see that the value is simply H(i)a. As H(0)a is 6a09e667, this means that our working variable for Round 1, H(1)b, will also be 6a09e667.
Moving along to H(i)c in the bottom row, we see that the arrow originates in the H(i)b box in the top row. Therefore the H(0)b value, bb67ae85, will become the working variable H(1)c in Round 1.
When we turn to H(i)d in the bottom row, we see that the arrow connects it to H(i)c at the top. Therefore, H(1)d is the same value as H(0)c, which is 3c6ef372.
Moving along, the arrow for the bottom H(i)e comes from the modular addition of H(i)d and the result that we got when we added the consonant. We figured out this value in the The modular addition never ends section, therefore the value for H(1)e is 0129560a.
The values for H(i)f , H(i)g and H(i)h are straightforward to figure out. If we follow the arrows from these values in the bottom row, we see that the arrows originate from H(i)e, H(i)f and H(i)g, respectively.
Therefore:
H(0)e, which was 510e527f, becomes H(1)f.
H(0)f, which was 9b05688c, becomes H(1)g.
H(0)g, which was 1f83d9ab, becomes H(1)h.
Just to recap, the working variables that we will use as some of our inputs for Round 1 are:
- H(1)a = 09b9f0ef
- H(1)b = 6a09e667
- H(1)c = bb67ae85
- H(1)d = 3c6ef372
- H(1)e = 0129560a
- H(1)f = 510e527f
- H(1)g = 9b05688c
- H(1)h = 1f83d9ab
Round 1 (and subsequent rounds)
We have finished Round 0 and we know what the working variables are for Round 1. If you refer back to the Converting to hexadecimal section, we also know the W value we need to use in Round 1:
W1 = 346E6720
You can also find the K value we need in the The constant, K, section. This time, we need the value in the second column of the top row:
K1 = 71374491
We now have all of the information we need to begin Round 1. First, let’s refer back to the diagram of the whole algorithm:
The SHA-2 algorithm
If we follow the arrows that come out of the bottom of Round 0, you will see that they point into Round t. Round t also has inputs of Wt and Kt. Round t is just a stand-in for each of the 62 rounds between Round 0 and Round 63, because drawing 64 rounds would have been impractical.
Instead, imagine that the arrows from Round 0 are really headed toward Round 1, and that the other inputs are really W1 and K1.
Now, let’s refer back to the diagram for a single round of SHA-2:
The SHA-2 calculations involved in a single round.
As indicated by the two diagrams, in order to complete Round 1, we simply have to repeat each of the operations we performed in Round 0. The only difference is that we are starting with different values. Instead of W0 we use W1. Instead of K0 we use K1. Instead of all of the H0 initialization variables, we use the H1 working variables. We have just listed each of these inputs that we need to begin Round 1, so you have all of the information you need to get started.
Your first step is to figure out Maj (a,b,c). This time, you need to use the new Round 1 inputs of:
- H(1)a = 09b9f0ef
- H(1)b = 6a09e667
- H(1)c = bb67ae85
We described the process in the The Maj operation section. It involved both AND operations and XOR operations, and we completed it through a number of steps using the online calculators. Once you have repeated the process with the new input values, you can figure out what to do next by either returning to the diagram or to the The ∑0 operation section of our article.
In this section, we performed a series of circular right shifts as well as XOR operations. This time, you need to use the new a value, H(1)a, which is:
09b9f0ef
The rest of the operations are the same, including the number of bits you need to shift. Once you have the result, it’s time to move on to the next step, which you can find by either consulting the diagram or referring back through the article. Once you have this result, you need to continue pushing forward, each time performing the same operations, but with the new input values wherever appropriate.
As a summary, to complete Round 1, you need to have:
- Performed the Maj operation.
- Completed the ∑0 operation.
- Used modular addition on these two prior results.
Then:
- Completed the conditional function.
- Finished the ∑1 operation.
- Performed modular addition on the result of the conditional function and the value for H(1)h
- Taken the result of the last step and added it to the result of the∑1 operation through modular addition
- Added this result to W1 through modular addition
- Used modular addition to take the result from the last step and add K1
- Added the result from the prior step to H(1)d with modular addition
Following these steps, you need to:
- Take the result you got when you added K1 (two steps ago), and add it to the solution you got from using modular addition to combine the results of the Maj operation and the∑0 operation (you got this answer in the third step, at the bottom of the first set of bullet points)
- Use the diagram and our descriptions in the The other working variables section to figure out which values will become the H(2) working variables that you will need for Round 2
Once you’re at this point, it’s time for you to start Round 2, this time using the H(2) working variables that you just figured out, alongside W2 and K2. Round 2 proceeds in the exact same manner, except it uses these new inputs where appropriate.
When you have finished Round 2, you will have the working variables you need for Round 3, and you will just need the W3 and K3 values that we listed earlier in the article to complete the operations.
This process repeats in Rounds 4 and 5 and so on, with the results becoming the working variables for the next round. The only complication comes in Round 16, where you must use the W16 value that we already calculated in the first Modular addition section, which was toward the beginning of the article.
The task becomes even more complex for Rounds 17 to 63, because you will have to calculate the W values yourself, using the method described in the other W values section and subsequent parts of the article.
Assuming you survive the ordeal and manage to make it to the end of Round 63, you will be left with eight H(i) values as your outputs from each of the calculations you completed throughout the round.
The final XOR
If you return back to the overall diagram of the SHA-2 function, you will see the final step:
The SHA-2 algorithm
You will see that the outputs from Round 63, which are the eight final H values that you would have figured out by this stage, all head into a series of modular addition boxes. These boxes also have other input arrows that trace back to H(i-1). This signifies that the other inputs in each of these modular addition operations are the initialization variables.
Therefore, you need to complete the following modular addition calculations:
- Final Ha value + H(0)a = d6320dec
- Final Hb value + H(0)b = c80c83e4
- Final Hc value + H(0)c = c17915ee
- Final Hd value + H(0)d = 5de8587b
- Final He value + H(0)e = b8118258
- Final Hf value + H(0)f = 759b2453
- Final Hg value + H(0)g = fce812d4
- Final Hh value + H(0)h = 7d3df56a
There’s only one thing left to do, which is to concatenate these results. This is just a fancy word for adding one to the end of the other in order. When you do this, you will be left with:
d6320decc80c83e4c17915ee5de8587bb8118258759b2453fce812d47d3df56a
The above result is our SHA-2 hash for “hashing is complicated”. In the diagram, this is represented by the Hi at the bottom.
Larger message inputs
If the initial message data had been larger than 448 bits, we wouldn’t be done yet. We would still need to process each of the remaining blocks until the entirety of the input data had been cycled through the SHA-2 algorithm.
If this was the case, we would not have concatenated our final results to form the hash. Instead, each of these eight Hi values would have become the initialization variables for the next block.
The steps would have proceeded much as above, except that this time our first 16 W values would have been portions of the second block of input data. The next 48 W values would have been derived from these 16 values according to the formula we used in the message schedule: finding the other W values section.
If there are only two blocks of input data in total that need to be processed, then after Round 63 of the second block, the final H values are added to the second block’s initialization variables in the same way that we just demonstrated for the first block. These results would then be concatenated to form the SHA-2 hash.
If there are more blocks, the Round 63 outputs from the second block would instead become the initialization variables for the third block. This process would continue until all of the blocks of input data have been processed. The eight outputs of the final block would then be concatenated into the SHA-2 hash, in the same way that we calculated the hash for a single block of input data.