This guide will cover the SHA-2 family of algorithms in broad terms. If you are looking for an in-depth dive into how the SHA-256 algorithm actually works, head over to our What is the SHA-2 algorithm? article.
SHA-2 is a family of cryptographic hash functions that includes:
- SHA-224
- SHA-256
- SHA-384
- SHA-512
- SHA-512/224
- SHA-512/256
The SHA-2 family of algorithms are used extensively in our online world, and make up a significant component of our online security. They are still considered safe in most applications, and are preferred over the insecure MD5 in the majority of use cases.
The applications of SHA-2
The SHA-2 family of hashing algorithms are the most common hash functions in use. SHA-256 is particularly widespread. These hash functions are often involved in the underlying security mechanisms that help to protect our daily lives. You may have never noticed it, but SHA-2 is everywhere.
To begin with, SHA-2 is involved in many of the security protocols that help to protect much of our technology:
- Transport Layer Security (TLS) — This is one of the most widely used security protocols. You will notice it most prominently when connecting to a website that begins with https rather than http. The s at the end stands for secure, which indicates that TLS is being used to encrypt the data between your device and the server. This makes SHA-2 an important part of many of the connections you make to websites when surfing online.
- Internet Protocol Security (IPSec) — IPSec is used to secure the connection between two points, and it’s most commonly seen in VPNs.
- Pretty Good Privacy (PGP) — PGP is one of the most popular protocols for encrypting emails so that they can only be read by the recipient. It protects the messages from hackers and other parties that may be able to read the data, such as your ISP.
- Secure/Multipurpose Internet Mail Extensions (S/MIME) — S/MIME is another prominent security protocol involved in email encryption.
- Secure Shell (SSH) — SSH is most commonly used for remotely accessing computers and servers, but it also has port forwarding, tunneling and file transfer applications.
In addition to being a core component of the above-mentioned security protocols, the SHA-2 family has a range of other uses. These include:
- Authenticating data — Secure hash functions can be used to prove that data hasn’t been altered, and they are involved in everything from evidence authentication to verifying that software packages are legitimate.
- Password hashing — SHA-2 hash functions are sometimes used for password hashing, but this is not a good practice. It’s better to use a solution that’s tailored to the purpose like bcrypt instead.
- Blockchain technologies — SHA-256 is involved in the proof-of-work function in Bitcoin and many other cryptocurrencies. It can also be involved in proof-of-stake blockchain projects.
- US Government data — Since 2015, the US National Institute of Standards and Technologies (NIST) has advised that all federal agencies should use either algorithms from the SHA-2 family or those from the SHA-3 family for most applications.
The history of SHA-2
The predecessors to SHA-2 were important stepping stones in arriving at the current algorithm. The National Institute of Standards and Technology (NIST) published the federal information processing standard (FIPS) 180 in 1993 for what we now refer to as SHA-0 in 1993. Weaknesses in the algorithm were discovered relatively quickly, so the algorithm was revised and an updated version, SHA-1, was released in 1995 with FIPS 180-1.
SHA-1 was also specified in RFC 3174.It was modeled closely on MD4, the 4th version of Ron Rivest’s Message Digest hashing algorithm.
The hash of SHA-1 is only 160 bits in length, which began posing security problems as technology and cryptographic techniques improved over time. This led NIST to introduce another update, which was outlined in FIPS 180-2. This document set out three versions of SHA:
- SHA-256
- SHA-384
- SHA-512
We refer to these algorithms as SHA-2. Despite the varying hash lengths, they all have the same underlying algorithm. In 2008, a 224-bit version of SHA-2 was added with the publication of FIPS-3, which delved into the algorithm’s details. SHA-2 is specified in RFC 4634.
By 2005, NIST announced its intention to phase out its approval for SHA-1 by 2010 due to the range of security issues that had been discovered.
Soon after, researchers published a paper that showed an attack where two separate messages could be found to result in the same SHA-1 hash in 269 operations, which was significantly lower than the previously presumed 280 operations. This showed that the security situation of SHA-1 was even more dire than had been thought, and pushed the community toward further adoption of the SHA-2 family.
What is a hash function?
Before we can go into the specifics of what SHA-2 is, we need to cover the basics. It’s not particularly useful to know that SHA-2 is a hash function with Merkle-Damgard construction if you don’t know what a hash function is yet.
At their most basic level, hash functions take inputs of any size and then convert them into fixed-length outputs, which are known as hashes.
The simplest hash functions are used for tasks like data retrieval and storage. One of the main advantages of these simple hash functions is that they allow data to be found and accessed within a short and consistent time frame.
We’ve covered how simple hash functions work in far more detail in our What is MD5 and how is it used? article. It goes into the basics of how these types of hash functions work, and covers why they are useful in greater depth.
What are cryptographic hash functions?
Cryptographic hash functions are special types of hash functions that have a range of strange properties. Not only do they change data of any length into fixed-length values, but they are also:
- Deterministic – This means that the same input always leads to the same fixed length hash as its output. When you enter, “hashing is complicated” into an SHA-256 calculator, you always get a hash of d6320decc80c83e4c17915ee5de8587bb8118258759b2453fce812d47d3df56a.
- Designed so that slight changes significantly alter the output – If you change the initial input by even a little, you will end up with a hash that seems completely unrelated. As an example, if we put “hashing is complicatedz” into the same SHA-256 hash calculator, we get a hash of 54afff2602d37e8dee0d696d7f6a352e8d1bae481b31cb50622b29b20594c2e5. As you can see, there doesn’t seem to be any overlap between this and the prior hash, despite such a subtle difference in the inputs.
- Fast to calculate – When you put an input into the SHA-256 calculator, the result seems to come up instantly (unless you have poor internet connection or an older device). When you consider each of the steps that take place in the SHA-2 algorithm, you may be surprised at just how rapid the whole process is.
- One-way functions – If you took either of the two hashes we have just shown you and you didn’t already know the initial inputs, it would be essentially impossible to figure out an input that results in either of these specific hashes. Using current techniques and technology, it’s considered so impractical to figure out a suitable input from just the SHA-2 hash that much of the world’s online security is built on the assumption that these attacks aren’t feasible. In this sense, these functions are one-way. It’s relatively easy to take an input and calculate the hash, but almost impossible to do the reverse.
- Collision-resistant – Cryptographic hash functions are designed so that it is unfeasible for two different inputs to result in the same hash. When separate inputs result in the same hash, it’s known as a collision, so the required property of these functions is known as collision resistance. While there are differing inputs that do result in the very same hash value, the likelihood of finding these needs to be almost impossible in order for a cryptographic hash function to be considered secure. If “hashing is complicated”‘s hash is 54afff2602d37e8dee0d696d7f6a352e8d1bae481b31cb50622b29b20594c2e5, it needs to be incredibly unlikely for anyone to be able to stumble across an input that results in this same hash, regardless of how much time they put into it.
What is SHA-2
Now that you know what a hash function is, and that the SHA-2 family is a specific subtype known as cryptographic hash functions, we can get into the more specific details of SHA-2.
As we have mentioned, SHA-2 is not just a single hash function, but a family of six. They are collectively referred to as SHA-2 because the family are the replacements to SHA-1, which was just a single algorithm. The SHA-2 family are as follows:
- SHA-224 – This version of SHA-2 produces a 224-bit hash. It has a block size of 512 bits, and the initial input is divided into 32-bit words for processing. The initialization variables are also 32 bits in length, as are the constants, K. Each block of data goes through 64 rounds of operations before the final hash (or the intermediate hash, in cases where multiple blocks of data are being processed) is produced.
- SHA-256 – SHA-256 results in a 256-bit hash and has a 512-bit block size. The message input is processed in 32-bit words, while the initialization variables and constants are also 32 bits in length. SHA-256 also involves 64 rounds.
- SHA-384 – This version produces a 384-bit hash. It differs from the prior two in that it has a 1,024-bit block size. It also varies in that it has 64-bit words, initialization variables and constants. Instead of 64 rounds, it requires 80 rounds of processing for each block of message data.
- SHA-512 – SHA-512 results in a 512-bit hash. Apart from that, it’s much like SHA-384 in that it has a 1,024-bit block size, 64-bit words, 64-bit initialization variables and 64-bit constants. However, the particular initialization variables it begins with are different from those in SHA-384. It also involves 80 rounds.
- SHA-512/224 – This version is much like SHA-512, except that it results in a truncated hash of 224-bits. This means that it involves a process that is largely the same, except that only the left-most 224 bits are taken as the hash, while the rest is discarded. The block size is also 1024 bits, while the words, constants and initialization variables are all 64-bits long. However, the initialization variables are different from those used in SHA-512 or SHA-384. SHA-512/224 also requires 80 rounds for each block of message data.
- SHA-512/256 – Like SHA-512/224, this iteration is also similar to SHA-512, except it produces a truncated 256-bit hash by only taking the left-most 64 bits. It has a 1,024 bit block size, as well as 64-bit words, constants and initialization variables. SHA-512/256 also has its own set of initialization variables. It involves 80 rounds.
You can view the specifics, including the values of each of the initialization variables and the constants in FIPS 180-4. Our What is the SHA-2 algorithm? article goes through every step of the process for SHA-256. If you are curious about one of the other versions of SHA-2, you can simply follow the steps for SHA-256 in our article, while changing the values to those specified in the FIPS 180-4 document.
The variations within the SHA-2 family
We have briefly introduced the six different SHA-2 functions and listed some of the differences between them. Now it’s time to go through what these differences actually mean:
Hash length
The above algorithms produce four different hash lengths:
- 224-bit
- 256-bit
- 384-bit
- 512-bit
The hash length is how long the hash is in bits. A 512-bit hash is much longer than a 22-bit hash, in a similar way that an eight-digit number is much larger than a four-digit number.
As a general rule, the smaller the hash length, the easier it is to find a collision, which is when two separate inputs result in the same hash. If you consider a hash as just a long number, which they basically are, this makes intuitive sense.
If we told you that we are thinking of a number that’s between one and five and you guessed that it was four, no one would be particularly impressed. If we told you that we were thinking about a number between one and a million and you correctly guessed that it was 984,287, our minds would be blown.
Why? Because it’s much easier to find a collision when we are dealing with a smaller range of numbers. Just as it’s much easier to guess a number between one and five than it is to guess one between one and a million, it is much easier find a collision for a hash that is between zero and:
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
Than it is to find one between zero and:
ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
*As a side note to those who are new to hexadecimal numbers. No, we did not have a seizure. The “f”s are actually numbers, but they are written in a system known as hexadecimal as opposed to the more conventional decimal numbers we use in everyday life. The decimal numbers you are used to are a base-10 system, which basically means there are 10 different numbers (0, 1, 2, 3, 4, 5, 6, 7, 8 and 9). You are probably somewhat familiar with another numbering system, binary, which is base-2, which means that there are only two options in the system, 0 or 1. Hexadecimal is a base-16 system, which basically means that there are 16 numbers (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, and f). This is why the SHA-256 hash that we have listed a few times has the letters a, b, c, d, e, and f in it. If you want to learn more about hexadecimal numbers, we have covered them in more depth in our What is MD5 and how is it used? article.
Now, let’s get back from our tangent and onto hash lengths once more. A longer hash is more collision-resistant than a shorter one. Despite this, each of the hash lengths in the SHA-2 family are considered secure in most applications.
The enhanced collision resistance of a longer hash comes with a trade-off. This is because the longer the hash, the more time it takes to calculate it and the larger the amount of computational resources it consumes. As technology progresses, it becomes more feasible to find collisions of larger hashes. In turn, our computational powers also increase over time, so it becomes more practical to use longer and more resource-intensive hashes.
Block size
The size of the block is also a compromise between security, speed and resource requirement. The smaller the block, the more blocks you will need to process a given data input (if the input is greater than the size of a single block). However, these smaller blocks will generally have a shorter computation time. There are additional factors that go into figuring out the most efficient block size for a certain scenario, but discussing the hardware intricacies and other aspects would take us off on too much of a tangent.
Both 512 and 1,024-bit block sizes are generally considered secure, but a given situation’s individual circumstances may lead to one or the other being chosen as the preferred size for implementation. Typically, you would want to use the minimum secure block size that suits the targeted operating environment.
Length of words, initialization variables and constants
If you refer back to the figures listed above in the What is SHA-2? section, you will see that the block size for each algorithm in the SHA-2 family is always sixteen times the size of the word length.
This is because the padded block of input data is always split between 16 words (a further 48 words are derived from these sixteen in the case of the SHA-2 algorithms with 512-bit block sizes. A further 64 words are derived for the algorithms with 1,024-bit block sizes).
This means that the words need to be one-sixteenth of the block size. In the case of the algorithms with 512-bit block sizes like SHA-224 and SHA-256, each word needs to be 32 bits long (512/16=32). The rest of the family each have 1,024-bit block sizes, and their word lengths are 64 bits (1,024/16=64).
One of the words is processed in each round, and in each round it is mixed in with the eight different initialization variables (after Round 0, newly computed variables are used in place of the initialization variables, which we refer to as working variables in our more detailed article on the algorithm through a number of separate operations). The constant is also added in the middle of these operations.
In the 512-bit block size versions of the algorithm (SHA-224 and SHA-256), the words, the constants, and the eight separate initialization/working variables used in each round are all 32 bits long. Alongside the modular addition (this is a special type of addition which we describe in more depth in our other article), this ensures that the outputs of each operation and each round are always the same consistent length.
The same goes for the four SHA-2 algorithms with 1,024-bit block sizes, except that all of the numbers are 64 bits long.
The reason for designing algorithms with either 32 or 64-bit word lengths has to do with speed and the hardware that these calculations are intended to be computed on. Ideally the register size of the CPU will match up with the word length.
Number of rounds
Each round of SHA-2 involves mixing up a portion of the message input (one of the words), with the initialization/working variables and the appropriate constant. It’s done through a complex series of operations. If you refer to our What is the SHA-2 algorithm article, you will see just how many steps are involved. It takes all the way from the The Maj operation section to the The other working variables section to discuss a single round of the SHA-256 algorithm.
As we mentioned earlier, one of the requirements of a secure cryptographic hash function is that it is a one-way function, which means that you cannot figure out the original input from the hash alone, nor can you figure out any input that could also produce the same hash.
To achieve this, the SHA-2 algorithm is essentially mixing up the input data with the constants and initialization/working variables, according to a very structured process. In this process, each round essentially serves to mix up the data even further.
A metaphor for rounds
Perhaps it would be helpful to visualize what’s going on in each round through a metaphor. Let’s say that you have two pages from the same newspaper. One is the front page and you are really interested in the main stories. The other page is just the classifieds, which you have no need for.
Let’s say that in the first round, you cut up each page into one hundred pieces. You then take a tenth of the front page pieces and throw them away. You replace them with a tenth of the pieces from the classified pages, and then mix them together. You now have two piles, one includes 100 pieces, which are mostly from the front page. The other pile contains 90 pieces of the classified page. At the end of this round, it might take you a little while, but you would probably be able to piece much of the front page back together and figure out what the headlines said if you wanted to.
In the second round, you cut all of the pieces of paper into two once again. You throw out another tenth of the pieces from the front page pile, and replace them with the same amount of pieces from the classified pile. Now you have 200 pieces of mostly the front page in one pile, and 160 pieces of the classifieds in the other. It would take you even longer now, but you would probably be able to reassemble much of the front page. You would probably still be able to figure out the headlines, or at least be able to make up another headline that fits in the gaps where letters are missing.
In the third round, you do the same thing once more, ending up with 400 pieces of paper in your front page pile, but now 30 percent of it from the classifieds. In the fourth round, you would have 800 pieces, but only 40 percent is from the original front page. By the fifth round it’s 1,600 and only 50 percent, while by the sixth you are dealing with 3,200 pieces, with only 40 percent of the original front page.
As you progress, it becomes harder and harder to reassemble the headlines, or to even come up with a headline that fits the remaining letters that you manage to put into the places.
This isn’t a perfect metaphor for the way that hash functions work, but the main point is that with each round, it becomes harder and harder to reassemble the original input, or even find any input that would fit. At some stage, you would simply say that it’s not feasible.
The above example is a lot like a one-way hash function. The headlines are kind of like the words of our input data that we process through the SHA-2 algorithm. The constants and the initialization variables are similar to the classified page. In both cases, it’s basically just extra meaningless data that gets mixed in with the input.
The rounds in both our metaphor and the SHA-2 algorithm also perform similar roles. They serve to mix up our input data with the meaningless data. After each round, the input data becomes more mixed up with the meaningless data, making it harder and harder to figure out the initial input, or any other input that would fit. Eventually, it gets to the point where it is simply impractical to figure out an input that may give the same result
Note that our metaphor produced an exponential rate of change after each round, where there were twice as many pieces at the end of each round as there were at the beginning. The SHA-2 algorithm does not divide the amount of data at the end of each round, nor does it increase the complexity at such a high rate with the processing of each round. If you keep this in mind, and that we are just demonstrating the concept rather than the rate of increase, the metaphor should still provide a good visualization of the role that rounds play in the SHA-2 process.
The main thing we are trying to get across is that the number of rounds in an algorithm impacts how feasible it is to figure out an input from the hash. If the SHA-2 algorithm was only one round long, the data wouldn’t have been mixed thoroughly and it wouldn’t be too hard to figure out an input that fits from the hash. With 64 rounds, it becomes so thoroughly mixed together that we don’t consider it feasible to figure out a matching input, while 80 rounds gives us an even greater margin of safety.
Truncation
SHA-512/224 and SHA-512/256 are mostly the same as SHA-512. While they each do use their own sets of initialization variables, the main difference is that the hash is truncated. This means that only the left-most 224 (or 256) bits are put out as the hash, and the other 288 (or 256) bits to the right are essentially discarded.
This truncation makes both SHA-512/224 and SHA-512/256 secure from length extension attacks. You see these attacks in applications where a secret value is added to input data, which is then hashed. These attacks are a concern in situations where the attacker has access to whatever the input data was, but not the secret value.
If vulnerable algorithms like MD5, SHA-1, SHA-256 or SHA-512 are used in hashing, length extension attacks may be possible. The attacker would need to know:
- Which hashing algorithm is being used.
- The victim’s data input.
- The hash of the victim’s data input.
If the attacker has this information, they may be able to reproduce a signature without ever having known the secret value.
This attack can seem a little abstract, so let’s look at a scenario where this could be problematic. Imagine a situation where a server authenticates a client based on this signature. The signature is a stand-in for the secret value, which the client obviously doesn’t want to share with the server, because it could lead to the secret value being exposed.
If the length extension attack allows an attacker to reproduce this signature without ever having known the secret value, it therefore allows the attacker to fraudulently authenticate themselves. In this way, hashing algorithms that are vulnerable to length extension attacks can result in the security provided by the secret value being undermined.
Now that we’ve covered the basics of length extension attacks, we can dive into how truncation prevents them. Length extension attacks require the hash of the victim’s data input in order to compute the signature. Truncated hashes like the ones produced by SHA-512/224 and SHA-512/256 do not contain sufficient information, because the outputs do not contain the rightmost 288 (or 256 bits).
Although SHA-512/224 and SHA-512/256 aren’t particularly common at the moment, their resistance to length extension attacks is a significant advantage. If an SHA-2 hash function is going to be implemented in a situation where these attacks are possible, either of these two algorithms may be the most secure option.
The SHA-2 algorithm’s design
Now that we have covered the differences between these SHA-2 variations, it’s time to look at the overall design of these hash functions. To start with, they are built from one-way compression functions.
SHA-2’s one-way compression functions
In cryptography, one-way compression functions take two fixed-length inputs and produce an output that is also a fixed length. The process makes it difficult to figure out what the two inputs were if you only have access to the output. The inputs do not have to be the same length, as we will see in SHA-2.
These one-way compression functions should not be confused with the compression algorithms we use to make audio, video and other files smaller.
For each block of data being processed by SHA-256, the one-way compression function has inputs of:
- 512-bits of message data — SHA-2 processes one block of data at a time. This input acts in a similar way that a key would in a normal block cipher (see the The SHA-2 block cipher section below). By this, we mean that it plays a controlling role in what the output will be. If there is more than one block of data that needs to be processed, these subsequent blocks become the inputs once the first block of data has gone through the SHA-2 algorithm. The final block must always be padded.
- One set of 256-bit initialization variables — These are broken up into eight parts for the initial processing of the first block. If there is more than one block, the 256-bit intermediate hash fills the role of the initialization variables in each of these rounds. The intermediate hash is essentially just the output from processing the prior block of data. These initialization variables and intermediate hashes take the place of the plaintext that would be encrypted in a normal block cipher (see the SHA-2 block cipher section below).
It produces an output of:
- One 256-bit hash — For a single block of data, the output of the compression function is the 256-bit hash. When processing multiple blocks of data, each block produces a 256-bit intermediate hash. As we mentioned above, these act as inputs for the next block. When all of the blocks have been processed, the output of the final block is the 256-bit hash.
Note that the compression functions in SHA-384, SHA-512, SHA-512/224 and SHA-512/256 each have inputs of:
- 1,024 bits of message data.
- One set of 512-bit initialization variables or a 512-bit intermediate hash.
They output:
- Hashes of either 384, 512,224 or 256 bits, depending on the algorithm. In the case of multiple blocks being processed, the intermediate hashes are 512 bits.
Compare the following two diagrams to see how SHA-2 uses its compression function:
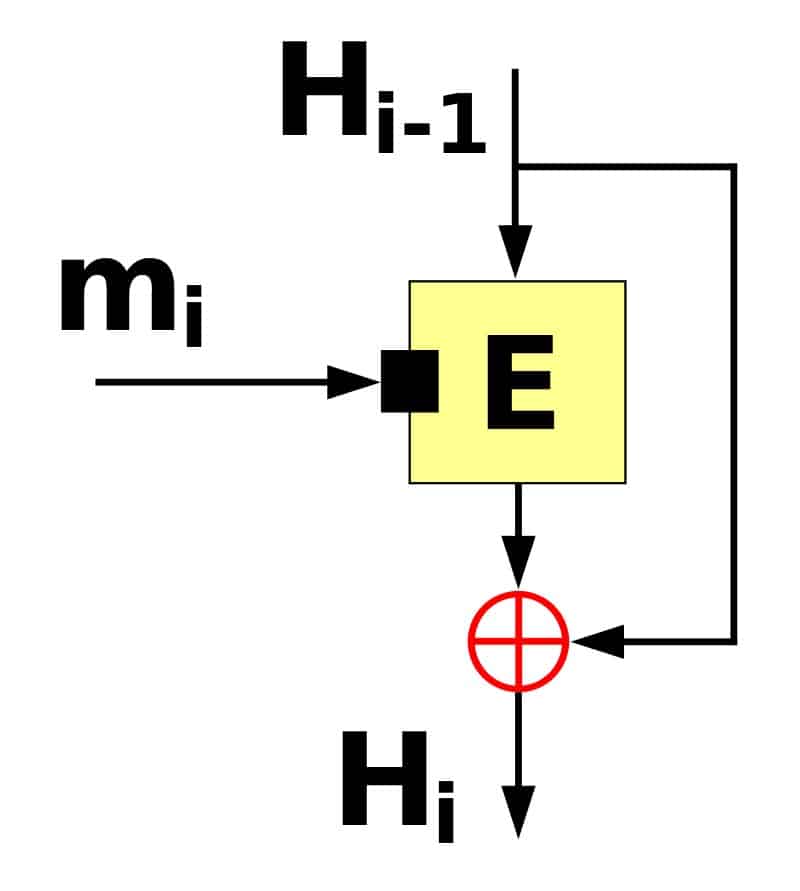
The type of compression function used in the SHA-2 algorithm. The Davies–Meyer one-way compression function by Davidgothberg licensed under CC0. 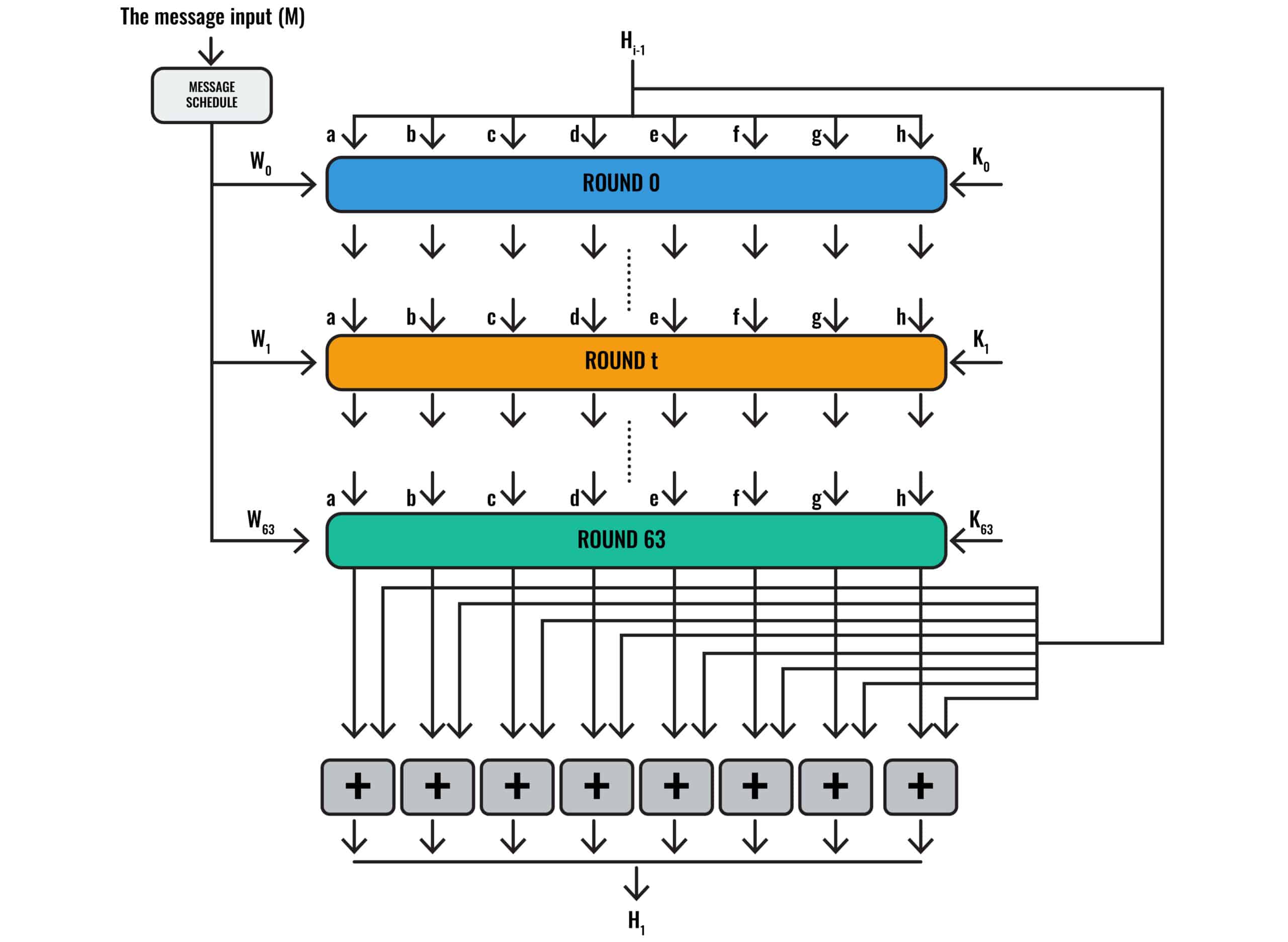
The SHA-2 algorithm for processing a single block
It may be hard to see the similarities between these two diagrams, because the second one has a lot more going on. Let’s start by explaining the parts that are easier to see.
You may notice that they both have Hi-1 at the very top. These Hi-1 inputs represent the initialization variables, or the intermediate hash from the prior block.
Both diagrams also share a Hi-1 at the bottom. These represent either the hash, or the intermediate hash that will be used in any subsequent blocks.
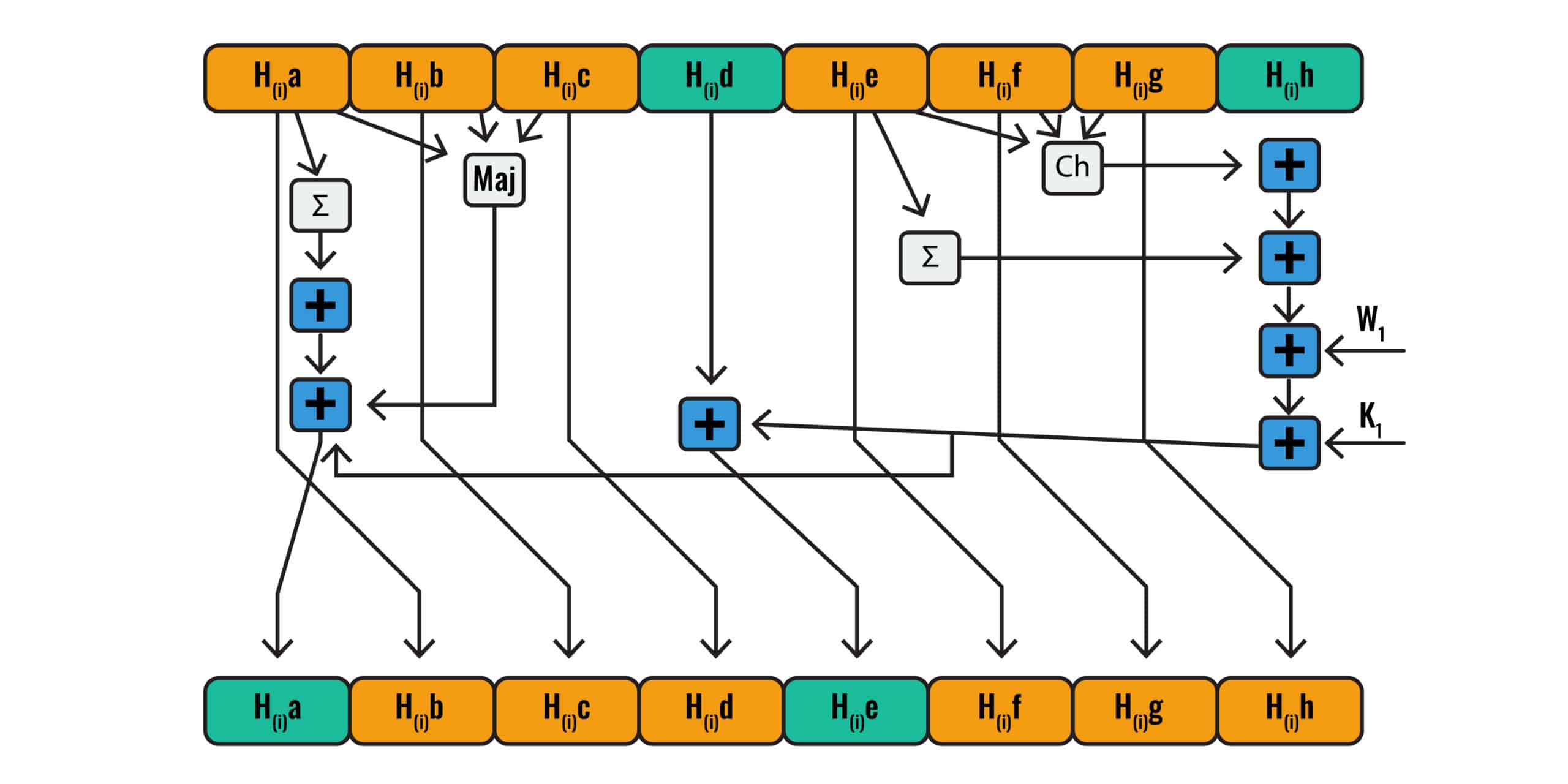
If you look at the second diagram, you will notice that we have the message input (M) at the top left. It goes through the Message Schedule, which has arrows pointing to each of the rounds. The message input (M) is our block of data, which gets split up by the Message Schedule.
The Round 0, Round t and Round 63 of the SHA-2 algorithm diagram are basically all encapsulated within the E of the compression function diagram. If you imagine that the eight plus symbols in the SHA-2 algorithm diagram represent the same thing as the circle with a cross in it in the compression function diagram, you will probably get a good idea of the role that one-way compression functions play in the SHA-2 algorithm.
Davies-Meyer compression functions
The particular one-way compression function that we have been discussing is a subtype known as a Davies-Meyer compression function. The defining feature is the arrow that goes from the Hi-1 directly to the red circle with the cross in it.
This represents modular addition (see the Modular addition section of our other article), where the initialization variables (or the intermediate hash from the previous block of data) are added to the output from E. Not all one-way compression functions have this feature.
To compare it to the in-depth example that we laid out in our other article, E represents the whole 64 rounds of processing applied to the 512-bit block of message data and the initialization variables. We covered the step that involved the circle with the cross in it in the final modular addition section of our previous article. It essentially involves adding the output of E to the Hi-1 value, which as we have stated, is either the initialization variables or the intermediate hash.
This Davies-Meyer structure has several advantages over alternatives like Miyaguchi-Preneel. Out of the other major alternatives, it is one of the simplest options. It also allows for the block size to be different to the size of the message input without the need for other additions to the algorithm. The Davies-Meyer structure gives the SHA-2 algorithm some efficiency benefits as well.
Merkle-Damgard construction
The one-way compression functions in the SHA-2 family are arranged according to Merkle-Damgard construction, which is a specific cryptographic hash function design. The aim of Merkle-Damgard construction is to make the hash function collision-resistant, meaning that it is unfeasible for an attacker to find two separate inputs that can both produce the same hash.
Why the collision resistance in Merkle-Damgard construction is important
Collisions are worrisome, because hashes are often used for digital signatures and other authentication processes. If an attacker can find collisions where two separate inputs result in the same hash, this opens up the possibility for them to fraudulently authenticate themselves.
One example involves an attacker carefully constructing two contracts that both result in the same hash, one that is legitimate, another that is fraudulent. The attacker would then show the legitimate contract to their boss and ask them to digitally sign it. Since the document is legitimate, the boss would sign it with their digital signature, which is based on the hash of the document plus the boss’s private key.
The attacker would then switch out the good contract with the fraudulent one and send it alongside the digital signature to their boss’s lawyer. The fraudulent contract could stipulate that the boss is signing over the rights for the boss’s house to the employee. The lawyer would then review the contract, and check the digital signature. Because of the employee’s mischief, the digital signature matches up. It would appear as though the boss had actually digitally signed the contract, so the lawyer would think it is legitimate and begin the process of handing over the legal rights of the home to the employee.
Of course, the original document that the boss signed would have been something completely different, and the only reason it appears legitimate is because the hash function involved in the digital signature process was not collision resistant.
The above example is a little extreme, but the point is that collisions completely undermine the security of our authentication systems, so we need to carefully design our hash functions to avoid them.
How does Merkle-Damgard construction work?
Merkle-Damgard construction involves compression functions, which can only handle fixed inputs. If the compression function is built to handle 512 bits of data at a time, you can’t just send 73 bits or 1,427 bits straight through it. You have to either pad out the data so that it takes up the entire 512 bits, or split up the data across multiple blocks and then add any necessary padding to complete the final block. Note that only the last block requires padding.
If you refer to the SHA-2 and padding section of our article on the SHA-2 algorithm, you will see that the first major step we took was adding padding to our message input data to make sure that our block sizes were all 512-bits long.
If you remember that the final 64 bits of the block were reserved to append the message length, this was because it’s a critical part of Merkle-Damgard construction.
This is known as length padding or Merkle-Damgard strengthening, and it serves to prove that a collision can only be found in the overall hash function if a collision can be found within the compression function. Remember, collisions are bad, and SHA-2 is a hash function that is built with compression functions. Essentially, what the proof is saying is that as long as the one-way compression functions are collision resistant, then we can also be confident that the overall hash function is also collision resistant.
The underlying proof involves a fair bit of math, but it basically shows that we can have this property in our hash functions if the padding scheme results in one padded message block never being the tail end of another. Appending the length as padding at the end of the final block of the input prevents this from happening, ultimately helping us prove the security of the hash function.
SHA-256’s Merkle-Damgard construction begins with a 256-bit initialization vector, which our other article describes as a series of eight 32-bit initialization variables. Our example only covers a single block of the SHA-256 function because of our small initial input, so we don’t really get to see how the Merkle-Damgard construction plays out across a series of blocks. Instead, the length padding is appended at the end of our one and only block.
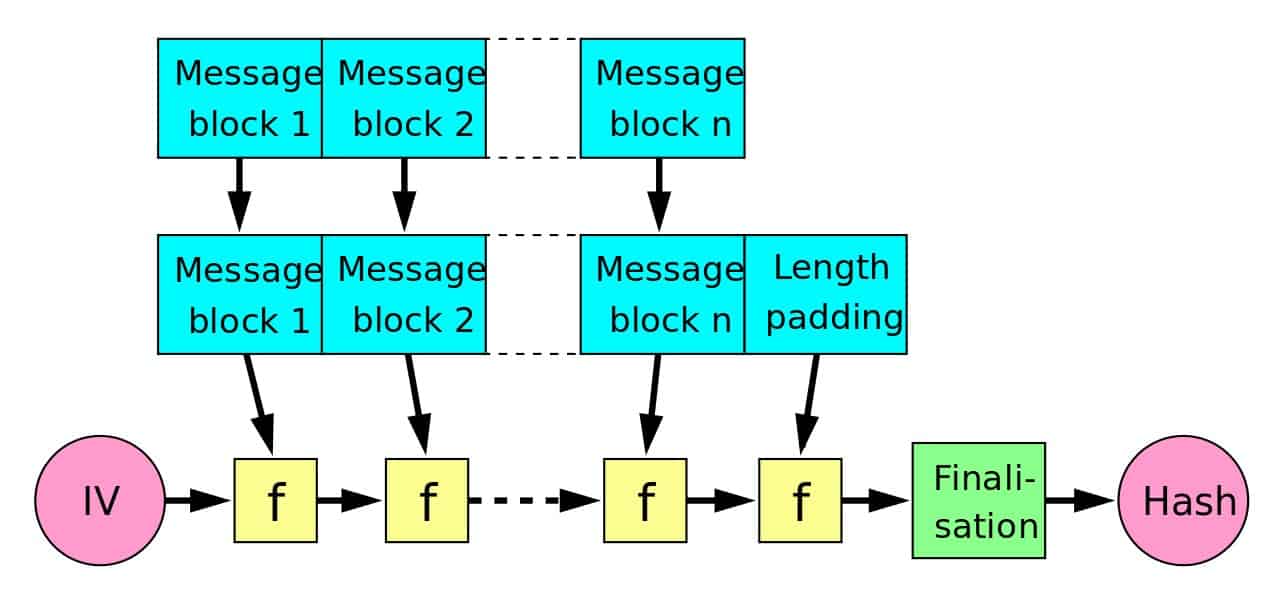
Merkle-Damgard hash construction by Davidgothberg licensed under CC0.
The SHA-256 algorithm.
The first diagram shows the design involved in Merkle-Damgard construction. The example we discussed in our other article only involved a single block of data, so it may be hard to see the resemblance between it and the Merkle-Damgard construction diagram.
It may be easier to understand Merkle-Damgard construction if we pretend that our message data was actually three blocks long. With this in mind, refer back to the first diagram. Message block 1 in the diagram would be our first 512 bits of message data. The IV on the left represents our eight initialization variables, which total 256 bits.
Both of these act as inputs to f. In the example from our other article, f would be the entire 64 rounds of operations on these two inputs, plus the modular addition involved in the Davies-Meyer compression function that we discussed earlier. This output would be the intermediate hash (or the set of eight working variables as we termed them in the other article).
Following the diagram along, this intermediate hash serves as an input into the second f function. Of course, our second block of message data would be Message block 2, which serves as the other input to the f function. The f function would simply repeat the same processing, except this time using the different inputs. It would result in a new intermediate hash.
This intermediate hash then becomes an input into our third block of message data. In this case, our other input would be Message block n, our third and final block of message data. Although it is somewhat separated in the Merkle-Damgard diagram, in SHA-2, this final block includes the padding and the appended message length that we discussed earlier.
The final stage of the Merkle-Damgard diagram shows the finalization function. The SHA-224, SHA-384, SHA-512/224 and SHA-512/256 algorithms compress their data in this stage. In the case of SHA-224, the 256-bits of output are compressed to a 224-bit hash. In the other three cases, the 512-bit outputs are compressed to 384, 224 and 256-bit hashes, respectively. This aspect is critical for mitigating the previously-discussed length extension attacks.
The SHA-2 block cipher
We’ve discussed the Davies-Meyer compression functions that are arranged in Merkle-Damgard construction to form the overarching structure of the SHA-2 family of algorithms. Now, it’s time to zoom in a little bit and look at the block ciphers that the compression function is built from.
A block cipher is more typically used in encryption, and involves:
- An input — This is normally the plaintext that needs to be encrypted.
- A key — A secret value that is supposed to only be known by those who are authorized to encrypt and decrypt the plaintext.
- An output — The encrypted data, which can only be read once it has been decrypted with the key.
While hash functions don’t really involve anything resembling decryption, the hashing process has some similarities to encryption. The Davies-Meyer compression function turns two input values (one can be seen as the plaintext, while the other can be seen as the key) and produces a single output, which is a lot like ciphertext.
The following diagram shows the SHA-2 block cipher:
The SHA-2 block cipher
Our other article outlines each of the steps in extensive detail, helping you to understand what happens in each box, and which values make up the inputs.
Is SHA-2 secure?
The SHA-2 family of algorithms is generally seen as secure, which is why it is recommended for most applications where a secure hash algorithm is needed. Each of the six algorithms are secure in most scenarios, however there may be certain instances where some are preferable over the others.
As an example, if length extension attacks are a threat, it may be best to go with either SHA-512/224 or SHA-512/256, as we discussed in the Truncation section of this article.
There has been significant research into the security of the SHA-2 family over the years, and no major problems have shown up. As an example of the academic community’s confidence in these algorithms, in 2016 researchers published a paper demonstrating the best attacks they could manage.
In the cases of SHA-512, SHA-512/224 and SHA-512/256, they were able to find collisions in only reduced 27-round versions of these algorithms. This is well short of the 80 rounds that they actually use, meaning that there is still a huge margin of safety and we don’t have to worry too much about their security at the moment. The other members of the SHA-2 family also have significant safety margins.
Alternatives to SHA-2
A more secure family of algorithms was released by the National Institute of Standards and Technology in 2015. Known as SHA-3, they are generally regarded as more secure than the SHA-2 family.
However, there has been limited uptake of the SHA-3 family, because there simply isn’t much of a need to change yet. As we mentioned, the SHA-2 algorithms still have a large safety margin, so there isn’t much force spurring institutions to update their hashing algorithms.
It’s nice to have SHA-3 in our back pocket, so that we have a set of algorithms to switch over to when the time is right. This should help to ensure a smooth transition. However, there’s simply not much of a need to take that leap for the foreseeable future.
Want to find out the details of how the SHA-2 algorithm works?
Now that you know what SHA-2 is, how its used, and that it is still considered secure, you may want to head over to our What is SHA-2 and how does it work? article. This piece goes into depth on each step of the algorithm, helping you understand how SHA-256 can turn a simple phrase like “hashing is complicated” into a jumble of letters and numbers like:
d6320decc80c83e4c17915ee5de8587bb8118258759b2453fce812d47d3df56a