Digital signatures are kind of like electronic versions of your handwritten signatures. They allow people to check the authenticity and integrity of data, as well as preventing the signatory from being able to repudiate (deny) their involvement.
These properties have led to the adoption of digital signatures in a wide range of applications, including many of our security protocols, secure email, and in digital rights management.
In this article, we will discuss what digital signatures are, where they are used, as well as the technical details of two of the most popular algorithms, RSA and DSA.
What are digital signatures?
As stated above, digital signatures provide us with three very important properties. These are authentication, integrity and non-repudiation.
Authentication is the process of verifying that the individual who sends a message is really who they say they are, and not an impostor.
The integrity of data or a message refers to whether it has arrived in the same state as when it was sent. If a message has been altered or tampered with, it no-longer retains its integrity.
If data or a message is non-repudiable, it means that its author cannot dispute that they were the true creator of the document. This property takes away plausible deniability, or the old “Sorry, my friend was using my account” excuse.
As long as the individual’s private key has not been compromised, digital signatures can provide all three of these properties to data.
You may be wondering why we need these properties in the first place. Let’s take a step back and think about how we do things in a face-to-face encounter.
Let’s say that you owe your friend Mike $100. You’re a good person, so you are happy to pay him back when you get the money.
The best way to do it would be to just give a $100 bill to Mike. You have known him for years and know what he looks like, so it would be easy to verify his identity and thus authenticate that you are giving the money to the right person.
If you were really anal, you could even check his ID and make him sign a handwritten receipt for you. The physical signature on the receipt would give it integrity and make it non-repudiable.
What about if, instead of doing the transaction face-to-face, you got a call from someone saying that they are Mike, and that you should send $100 to account number 12345678.
“But you don’t sound like Mike,” you say.
“I have a cold. Send it now, I need the money.”
Would you send the money? Probably not.
There is no way to know whether it really is Mike or the correct account number. For all you know, it could be an impostor who is trying to steal from you. Instead of transferring the money immediately, it would be best to wait until you see Mike so that you can give him the cash in person.
Just like in the above scenario, we frequently run into situations where we need to verify the identity of a party or the integrity of data in the online world. That’s why digital signatures have risen as a mechanism that can provide these properties and facilitate secure online transactions.
Without them, we may not know who we are talking to, could not be sure whether or not data has been tampered with, and the person could deny that they were responsible.
The uses of digital signatures
These properties of digital signatures make them useful in a wide variety of applications. They are often used by themselves or in conjunction with encryption in a range of different security protocols, such as:
They are also frequently used in digital rights management, in blockchain technology, in contract management applications, as part of software distribution, and in finance.
History of digital signatures
The idea of digital signatures was first floated by renowned cryptographers Whitfield Diffie and Martin Hellman in their 1976 paper New Directions in Cryptography. In 1978, Ronald Rivest, Adi Shamir and Len Adleman brought the RSA algorithm into public view, which could be used to produce insecure digital signatures.
It took another decade for digital signatures to emerge in a widespread application: the release of IBM’s Lotus Notes 1.0. From then onward, digital signatures began to see wider adoption as new techniques emerged and the need for online authentication and integrity checks grew.
A brief intro to public-key cryptography
Before we jump into digital signatures, it’s best to cover some of the important aspects of public key cryptography, which form the basis of how digital signatures work.
If you are relatively new to cryptography, the system that you will be most familiar with is symmetric-key encryption. This just means that the same key (which is similar to a password, but has some differences) is used to both encrypt and decrypt data.
Public-key encryption was a revolution, because it involved using separate keys for the encryption and decryption process, leading to a range of different cryptographic applications. These two keys formed a key pair, made up of the public key and the private key. The public key can obviously be shared publicly, while the private key must be kept secret in order for the system to be secure.
The two most common uses of public-key cryptography are encryption and digital signatures.
Encryption
One of the groundbreaking features of public key cryptography was that it allows parties who have never met to confidentially send messages to each other. The sender seeks out the public key of their desired recipient (these can be found on public key servers, on personal websites, or simply by asking the individual), then encrypts a message with this key, before sending it to the recipient.
The recipient is the only person who can access the message—assuming that the private key has not been compromised—by decrypting it with their private key. Even though the public key was used to encrypt the message, it can only be decrypted by the private key. If the recipient wishes to reply, they find the public key of the original sender, then repeat the process.
See also: Common encryption types explained
How do digital signatures work?
As we have said, digital signatures are used for authentication, to see whether data has been tampered with, and to provide non-repudiation. There are a range of different mechanisms that can be used for digital signatures, and they each have slight variations in how they are structured.
In general, these algorithms need to be composed of three sub-algorithms:
- A key generation algorithm – This algorithm generates a random key pair for a user. The numbers involved in the key pair need to abide by certain parameters to be considered secure. Two of the most important aspects are that the numbers are sufficiently random and adequately sized.
- An algorithm for signing data – Once a user has their keys, there are specific ways for how they are applied to data in the signature process.
- An algorithm for verifying the signature – Likewise, verifying a signature follows a predetermined process.
For a digital signature system to be effective, it needs to be structured in such a way that:
- Data signed with a private key is verified with the same individual’s matching public key.
- It should be essentially impossible (using current technology and techniques) to forge a valid signature without knowing the individual’s private key.
Some of the most common digital signature schemes include RSA, DSA, EcDSA and EdDSA.
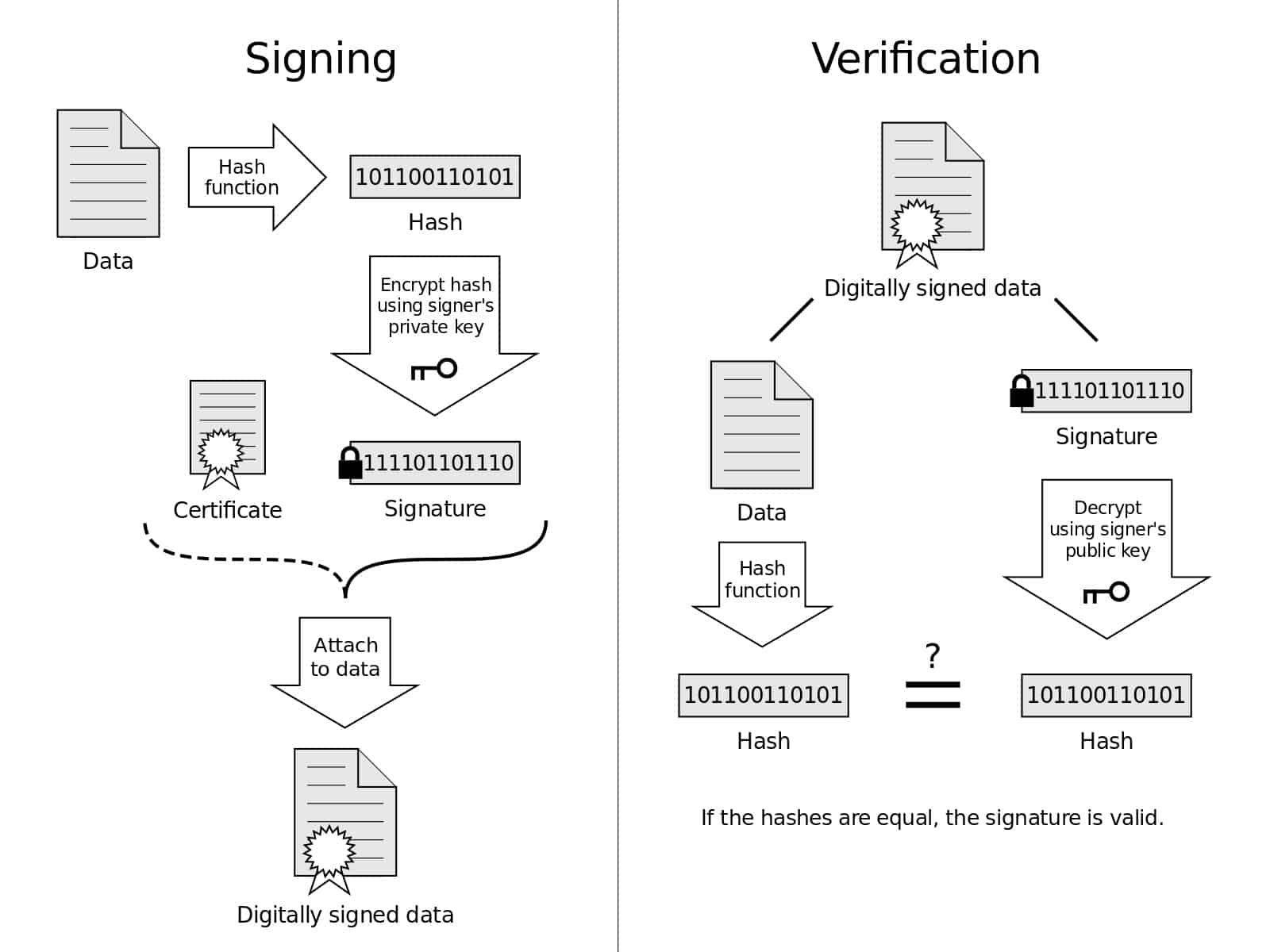
This image gives a visual representation of the signing and verification processes. Digital Signature Diagram by Acdx licensed under CC0
RSA
RSA was the first digital signature algorithm, but it can also be used for public-key encryption. In this article, we will skip over the encryption aspect, but you can find out more about it in our comprehensive article that covers what RSA is and how it works.
RSA key generation
In secure implementations of RSA, key pairs will generally be established automatically under the following process:
Prime generation
Two individual prime numbers are selected, p and q. The exact size of these primes will vary depending on the key size. These days, a minimum of 2048-bit RSA keys are generally recommended for adequate security, so we are talking about two prime numbers that multiply to produce a 2048-bit number.
2048 bits is a size in the binary number system. If a number of this size was converted to our more familiar decimal system, it would be approximately this long:
790279459827301874397592846209502937592870495029380589710393
7019019209839375970193850891039510730584153687576287365984259
3824756984376582763487912837582736592873684273684728938575872
4958729873958729835792875982795837529876348273685729843579348
7958458720948602984912837502948019371092482793857928739548772
3975928375924785938670358103799581093750193850791345986792384
7378267352673547623568734869386945673456827659493849024875809
6039429837592834759348759384759284780634701938091803984091804
9810938592873995710901985013984019835091835019830910791803958
1039519039518093581093850198401935801938401983409180938510983
09180019
The primes in RSA must be selected randomly and should have similar lengths.
In our example, we will use much smaller numbers to make things easier to understand. Be aware that using keys of this size would make the digital signatures trivial to fake. This is why such large values are used in practice.
Let’s say that:
p = 13
q = 17
The first step would be to calculate the modulus n using the following formula:
n = pq
n = 13 x 17
n = 221
The value of n is also the key length.
Carmichael’s totient function
Now that we have the value for n, the next step is to use Carmichael’s totient function:
λ(n) = lcm (p − 1, q − 1)
There are a few things that you need to understand:
- λ(n) means Carmichael’s totient for the value of n
- lcm represents the lowest common multiplier. This is the lowest common number that both p-1 and q-1 can divide into
Let’s plug our figures into the equation:
λ(221) = lcm (13 − 1, 17 − 1)
λ(221) = lcm (12, 16)
If you are good at mental math, you may have figured out that 48 is the lowest common multiplier of both 12 and 16. This is because 48 is the smallest number that both of these numbers can fit into (12 x 4 = 48, 16 x 3 = 48). Therefore:
λ(221) = 48
Coming up with the public key
In RSA, the public key is comprised of the value n (which we have already calculated as 221) and e. Since the public key is freely shared, the value for e doesn’t have to be a secret. In fact, it’s often set to 65,537 in practice, because larger numbers would slow down the encryption process. In our example, we’ll set e to 5, just to make it a small and simple number to work with.
Therefore, the public key for this example is comprised of 221 and 5. We will cover the specifics of how the public key is applied in the following sections.
Figuring out the private key
Just as our public key is made up of two numbers, so is our private key. Private keys are comprised of d and e. We already know the value for e (5), and we can use the following formula to find d:
d =1/e mod λ(n)
Note that mod just symbolizes a modulo operation, which would normally mean that you have to find the remainder once you divide the left side by the right. As an example:
17 mod 3 = 2
This is because 3 fits into 17 a total of 5 times, with a remainder of 2.
Our example is a little bit different. The “1/e mod” segment of the equation may appear to be telling you to divide 1 by e, but it actually isn’t. It’s confusing, but this is a way of representing the modular inverse. The equation is actually telling us to calculate the modular inverse of e and λ(n).
The modular inverse is normally derived using the extended Euclidean algorithm, but we won’t be covering that in this article. Instead, we will just use an online calculator to make things easier.
Now that we’ve gotten that out of the way, let’s enter our values into the formula:
d =1/5 mod 48
To find d, all that we have to do is enter our value for e (5) into the online calculator where it says integer, then our value for λ(n), which is 48, where it says modulo.
This gives us a result of 29 according to the online calculator. Therefore, our private key will be made up of:
e = 5
d = 29.
Now that we have generated both of our keys, the next question is, “What do we do with them?” Well, we could use them to encrypt and decrypt messages through public-key cryptography, but this article is about digital signatures, so we’ll focus on that.
Digitally signing data with RSA
Let’s say that someone wants to send a message to their friend, but they want to make sure that the friend can verify the authenticity and integrity of the message. They could do this by using an RSA digital signature to sign the message.
The first step is to run the entire message through a hash function. These are one-way functions which always deliver the same output for a given input. Secure hash functions are essentially impossible to reverse, which means that the output cannot be used to figure out the input. It is also infeasible for two separate messages to have the same output.
You can find out more about hash functions in the What is hashing? Section of our Encryption, hashing, salting – what’s the difference? article.
Let’s say that we want to digitally sign the message “It’s hot today” so that our recipient can know whether the message is authentic or not, and if it has been tampered with. We would start by running “It’s hot today” through a hash function.
Understanding hash functions
These days, the most commonly used secure hash function is SHA-256. When we put our message through an online SHA-256 calculator, it gives us a result like this:
efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952
This raises a few problems for our example. The first is that it isn’t a decimal number like those that most people are used to. You may have noticed that there are letters in this number, and that they only go up to f. This gives us a clue that it’s actually a hexadecimal number.
The hexadecimal system relies on a base of 16, rather than a base of 10, like the number system that we normally use. This means, that instead of counting in multiples of 10, it counts in multiples of 16, and the first 6 letters of our alphabet are used to make up these extra numbers. A number like this can be converted into our everyday decimal system, but that’s out of the scope of this article.
The second issue that we have is that this is a really big number. If it was converted to decimal, it would be even longer. Since we are aiming for simplicity in this guide, running the calculations with such a large number would make things too confusing to get the basic concepts across.
With the idea of demonstrating how RSA digital signatures work in a manner that is easy to understand, we won’t be using such a large hash value in the following example. Instead, we will pretend that the hash value of “It’s hot today” is simply 10.
We will also have to pretend, that like any real hash, whenever we put our input of “It’s hot today” through the hash function, it will always return the value of 10. To be consistent with how hash functions normally work, we will have to pretend that it’s incredibly unlikely for any other input to give the same value. Similarly, we need to pretend that it’s also not feasible to figure out our original input from this value. These properties are what make hashes immensely useful.
How the sender’s private key is used to digitally sign the hash value
Our sender has typed out their message, then put it through a hash function, which we are pretending returned a value of 10. Once the sender has the hash of the message, they can create the digital signature by applying their private key to the hash value with the following formula:
m (c) = cd mod n
This is actually the formula for decrypting data that has been encrypted with the recipient’s public key, but it’s also used for digitally signing documents.
When it comes to digital signatures:
- The value of m (c) will be the signature.
- The value of c is the hash of the message (10).
- The value of d is part of the sender’s private key, which we derived earlier (29).
- The mod function is the same remainder operation that we covered earlier.
- The value of n is the other part of the sender’s private key, which we calculated at the start (221).
So, let’s put it all into our formula:
m (c) = 1029 mod 221
m (c) = 100,000,000,000,000,000,000,000,000,000 mod 221
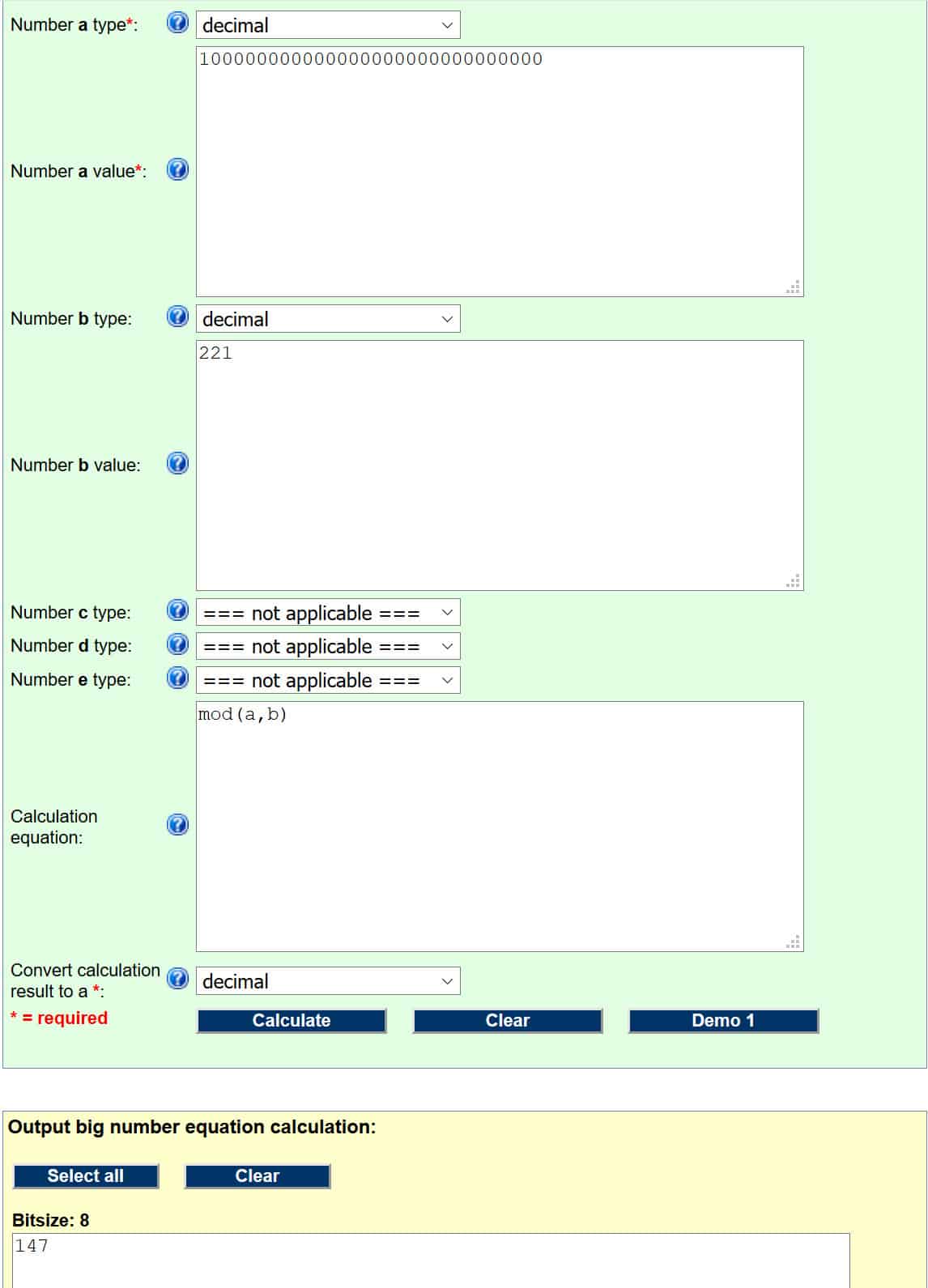
Let’s run this through the following modulo calculator (we explained how these operations work under the Figuring out the public key section). For it to work properly, we need to set our inputs as:
- Number a type – decimal
- Number a value – 100000000000000000000000000000
- Number b type – decimal
- Number b value – 221
- Calculation equation (this is just the code that tells the calculator which operation to perform. This and other codes can be found on the webpage linked above the input section) – mod(a,b)
If you have done things properly, it should look like this:
The number in the yellow box is our answer, so the digital signature for the hash of the message is 147.
To prove the authenticity and integrity of the message, along with providing non-repudiation, our sender would transmit the message “It’s hot today” alongside the digital signature of 147 to their desired recipient. Just remember that we used a small value for the hash to simplify things, instead of the real hash of the message.
Verifying digital signatures
Digital signatures are only useful if we can verify whether they are legitimate. As long as a sender’s private key has not been compromised, the recipient can test whether a message is authentic and retains its integrity by applying the following formula to the digital signature:
c(m) = me mod n
In a reversal of the signing process, this is actually the formula that is used to encrypt data in RSA. When we use this formula to verify signatures:
- The value of c(m) will be the sender’s hash value at the time they signed it (due to the structure of the RSA public-key algorithm, applying the sender’s public key through this formula will undo the signing operation that we just performed, leaving us with our original pretend hash).
- The value of m is the digital signature (147).
- The value of e is part of the sender’s public key, which we derived earlier (5).
- The mod function is the same remainder operation that we covered earlier.
- The value of n is the other part of the sender’s public key, which we calculated at the start (221).
Let’s throw it all into the formula:
c(m) = 1475 mod 221
c(m) = 68,641,485,507 mod 221
Let’s use the same modulo calculator as before and keep everything the same, except:
- Number a value – 68,641,485,507
If you have entered things correctly, you should get a result of:
c(m) = 10
Now that the recipient has calculated the hash value from the digital signature, their next step is to calculate the hash value of the message that they received, “It’s hot today”. If you remember from earlier, we didn’t actually use the real SHA-256 hash of the message, because the number would have been too big and made the example too complicated.
Instead, we have been pretending that the hash function actually gave us the small number, 10, for our input. Since hash functions always output the same result for a given input, when our recipient puts “It’s hot today” through our imaginary hash function, they also would have received the value of 10.
The signature verification process results in two values. The first value is the hash as it was when the sender digitally signed it with their private key. We calculated this above using the sender’s public key.
The second value is the hash of the message that the recipient received. This is calculated by using the same hash function that the sender used to hash their original message. These two values are then compared, and if the values are the same, then we can assume that the message is authentic, retains its integrity, and that it is non-repudiable. Of course, this assumes that the sender’s private key has not been compromised.
Since our example returned a value of 10 for the hash when it was signed by the sender, as well as a value of 10 as the hash of the message that was received, we can assume that the message, “It’s hot today” comes from the person who claims to have sent it, and that it has not been altered since it was sent.
If the recipient wants to respond so that their correspondent can verify their message in the same way, the whole process is repeated, except the recipient’s private and public keys are used for the signing and verification processes, respectively.
All of this math may have put you off the whole idea of digital signatures. Don’t worry, because implementations of RSA automate this process, so you don’t have to crunch any numbers.
RSA pros & cons
RSA is one of the most widely-supported and implemented digital signature algorithms, although there is a move towards the newer, more efficient and secure algorithms such as ECDSA and EdDSA.
When compared with DSA (which we will cover in the next section), RSA is faster at verifying signatures, but slower at generating them. Since signatures tend to be created once and verified many times, RSA is generally preferred over DSA.
DSA
The security of the Digital Signature Algorithm is based on two mathematical concepts, the discrete logarithm problem, and some properties of modular exponentiation. For some groups, it is infeasible to compute their discrete logarithms with current techniques and technology.
DSA key generation
To generate DSA keys, the first step is to choose the parameters which a group of users in the same system can use to generate a key pair.
Generating the parameters
- Choosing a hash function – SHA-256 is the most common option to meet modern security requirements.
- Settling on key lengths, L and N – These days, L should be at least 2,048 bits long, while N should be at least 256 bits.
- Decide on a prime, q, that is the same length as N.
- Select a prime, p, where p-1 is a multiple of q.
- Pick a number, g, using the following formula (where h is an arbitrary number between 1 and p-1):
g = h(p − 1)/q mod p
Normally, these values are very large numbers in order to make the algorithm secure. To keep our example from being too difficult to compute or explain, we will use much smaller numbers that would not actually be secure. Let’s say that:
q = 5
p = 11
To find g, we plug our numbers into the formula. We will use 3 as our value for h:
g = 3(11-1)/5 mod 11
g = 32 mod 11
g = 9 mod 11
We will use the same modulo calculator as in the How the sender’s private key is used to digitally sign the hash value section. The parameters will be the same, except:
- Number a value – 9
- Number b value – 11
If you have entered everything correctly, it will give you a result for g of 9.
Generating the user keys
Individual users then take these parameters and use them to form their key pair:
- The private key (x) is a number in between 0 and q, which we set at 5. For our example, we will choose 2 to be x, our private key.
- The public key (y) is calculated using the following formula:
y = gx mod p
Therefore:
y = 92 mod 11
y = 81 mod 11
We will use the same modulo calculator once more. The parameters will be the same, except:
- Number a value – 81
- Number b value – 11
If you have entered things correctly, you should have gotten a result of y = 4. The public key is therefore 4.
Now that we have generated all of our values, let’s give you a quick recap. The parameters for the system are:
- p = 11
- q = 5
- g = 9
Our key pair is made up of:
- The private key, x = 2
- The public key, y = 4
Digitally signing data with DSA
Senders can use their DSA private key to digitally sign electronic documents or digital messages, which allows their recipient to verify whether the data is authentic and retains its integrity. It also prevents the sender from being able to repudiate the message.
The signature process starts by generating a random value k, which is between 1 and q. For this example, let’s just choose 3 as our “random” number, k.
We then follow the following formula to create an individual key (r) for the message:
r = (gk mod p) mod q
Let’s throw in our numbers:
r = (93 mod 11) mod 5
r = (729 mod 11) mod 5
We use our modulo calculator again, entering 729 and 11, which gives us a result of 3. Therefore:
r = 3 mod 5
And then we repeat the modulo operation again with the new values to give us:
r = 3
Our value for r is used as the key for the message.
We come up with the other part of the digital signature, s, with the following formula:
s = k-1(H(m) + xr) mod q
The k-1 does not represent taking the negative power of k, but instead calculating the modular inverse, just like in our Figuring out the private key subsection in the earlier part of the article where we talked about RSA.
H(m) is the hash value for the message that the sender is signing. Normally, this would be a long hash value that was derived from the message, just like in the Understanding hash values subsection above, which we covered when we were talking about the RSA algorithm.
For this example, we will keep things simple. Just like in the RSA section, we will say that our message, m, is “It’s hot today” and that the hash of the message H(m), is 10.
So let’s enter all of our values into the formula:
s = 3-1(10 + 2 x 3) (mod 5)
s = 3-1(10 + 6) (mod 5)
s = 3-1(16) (mod 5)
Now, we take the modular inverse of 3 for the order of 5 (because 5 is our value for q), using the same modular inverse calculator from earlier. Enter 3 as the integer and 5 as the modulo, which will give you a result of 2. Therefore:
s = 2 (16) (mod 5)
s = 32 (mod 5)
Let’s go back to our calculator for the normal modulo operation, keeping the same parameters that we used earlier, except:
- Number a value – 32
- Number b value – 5
If you have done this correctly, it will give a value for s of 2. The digital signature is composed of r and s (3 and 2, respectively). The senders transmits the digital signature to their recipient alongside their message, “It’s hot today”. They will also share the values of p, q, g and y with their recipient.
Verifying digital signatures
When the recipient receives the digital signature alongside the message, they can verify the message’s integrity and authenticity with the following set of calculations.
The first step is to find the hash of the message that they received. The recipient does this by running the entire message through a hash function. To keep things simple and consistent, let’s say that the hash of the message, H(m) is 10.
The recipient has also been sent the following values, which they use in the verification process:
- The digital signature (r, s) – 3, 2
- p – 1
- q – 5
- g – 9
- y – 4
The first calculation is to find w:
w = s-1 mod q
Again, the s-1 represents taking the modular inverse. Let’s enter our values:
w = 2-1 mod 5
We will use the modular inverse calculator from earlier. Enter 2 as the integer and 5 as the modulo, which will give you a result of 3 for w. The next step is to find u1 with the following formula:
u1 = H(m) x w mod q
Let’s throw in our values:
u1 = 10 x 3 mod 5
u1 = 30 mod 5
Back to the normal modulo calculator, keeping the same parameters that we used earlier, except:
- Number a value – 30
- Number b value – 5
This gives us a result of 0 for u1.
We use the next formula to come up with u2:
u2 = r x w mod q
Let’s enter our numbers:
u2 = 3 x 3 mod 5
u2 = 9 mod 5
We then head back to the normal modulo calculator, using the same parameters as earlier, except:
- Number a value – 9
- Number b value – 5
If you enter this correctly, it will give you a result for u2 of 4.
Now that we have our values for u1 and u2, we can find v, with the following formula:
v = (gu1yu2 mod p) mod q
Let’s throw in our numbers:
v = (90 x 44 mod 11) mod 5
v = (1 x 256 mod 11) mod 5
v = (256 mod 11) mod 5
We go back to our normal modulo calculator, using the same parameters as earlier, except:
- Number a value – 256
- Number b value – 11
This gives us a result of 3. Therefore:
v = 3 mod 5
Then we use the normal modulo calculator one final time, again with the same parameters, except:
- Number a value – 256
- Number b value – 11
This gives us a result for v of 3.
If the message is authentic and hasn’t been tampered with, then v will be equal to r:
v = 3
r = 3
3 = 3
Therefore the message was sent by the owner of the private key, and the message has not been altered since it was signed.
DSA pros & cons
The security of DSA is reliant on whether it uses adequate numbers. In addition to p, q and g abiding by the correct parameters, the value of k also needs to be random. It should not be a predictable value, or a value that is used multiple times. If these requirements are not met, then the key can be recovered by an attacker.
Despite this possibility, DSA is generally considered secure as long as it is implemented correctly and it uses adequate values. Even though it is relatively secure, DSA doesn’t tend to be implemented much compared to RSA or the other digital signature methods. When compared with RSA, it can generate keys faster and is also quicker at generating digital signatures, but slower at verifying them.
Version 7.0 of OpenSSH stopped supporting DSA keys by default, which seems to be a sign that the world is moving past DSA and on to other algorithms.
ECDSA & EdDSA
RSA and DSA aren’t the only digital signature algorithms, nor are they the most suitable for all situations. There are a range of others, such as ECDSA and EdDSA, which have properties that make them preferable in certain circumstances.
Unfortunately, these rely on even more complicated math, such as elliptic curve and Edwards curve cryptography. We won’t be covering them in detail due to their added complexity, but we will talk about some of their potential positives and negatives.
ECDSA
The Elliptic Curve Digital Signature Algorithm is a variation of DSA that incorporates elliptic curve cryptography. It provides a similar level of security to RSA, but with a much smaller key. This makes it more efficient than RSA or DSA in most aspects of performance.
EdDSA
This is another DSA alternative, except it is based on Twisted Edwards curves. It is relatively new as far as algorithms go, which has both its advantages and disadvantages. On the positive side, it uses newer techniques that add to its performance.
Unfortunately, newer algorithms haven’t been exposed to as much scrutiny, so many people are cautious when deciding whether or not to implement them.
Despite this, the use of EdDSA provides a high-level of performance, resistance to side-channel attacks, and does away with the need for a unique random number in each signature. At this stage, EdDSA looks promising and it is starting to see wider implementation, but we will have to wait and see whether future studies find any security holes.
Digital certificates
Anyone can easily make a key pair, even an attacker. So what keeps someone from making a bunch of keys and pretending they are the President, or posing as anyone else?
Well, nothing stops someone from claiming that they are another person, but there is a system in place that allows others to ascertain whether or not the person truly is who they claim to be.
It’s called the public key infrastructure (PKI), and it involves digital certificates that link an individual or entity’s public key to their true identity. These certificates are signed by others to indicate just how much the certificate should be trusted.
You can compare the process to using notaries to verify documents. If someone has a copy of a birth certificate, you may be skeptical about whether or not it is legitimate. If that same birth certificate was signed and stamped by a notary, you would be much more likely to believe that it is a real copy.
Why?
Because the signature and stamp show that a trusted public entity has seen the individual and their original birth certificate, then verified that the copy is in fact legitimate. The notary validates the copy of the birth certificate and stakes their reputation behind it with their signature and stamp.
The trust that we have for the notary gets transferred to the copy of the birth certificate, allowing us to trust it far more than one which has not been notarized.
There are two major types of certification, certificate authorities (CAs) and the web of trust.
Certificate authorities
Certificate authorities are trusted organizations that run checks on individuals or entities to verify whether they are the legitimate owner of a public key. If the checks reveal that the individual is the true owner, then the certificate authority will sign the certificate with its own key, signifying that it has completed the check and believes that the individual and public key are legitimately linked.
As long as we trust the certificate authority and their process of verifying the key, then we can trust a certificate that has been signed by them, and thus that the public key truly represents that individual.
Depending on the type of certificate and its application, different levels can have varying verification processes, and thus either represent a higher or lower degree of trust.
The web of trust
The web of trust operates under a similar premise, except there are no central bodies like certificate authorities that perform the verification process and sign the certificates.
Instead, the web of trust relies on other individuals to sign certificates, staking their reputations on the link between the individual and the public key. This system is mostly used with PGP, where users can easily make their own certificates.
It works like this:
Let’s say you have two friends who want their certificates signed to prove that they are the legitimate owners of their respective public keys. You know these people well, and they show you their government IDs, which makes you absolutely certain that they are who they say they are, and are thus the true owners of the public keys they are claiming.
Since you know that they are the legitimate owners of their public keys, you are happy to use your private key to sign their certificates, staking your reputation on them and essentially saying “Yes, I have verified the identities of these individuals and they are who they claim to be”. These two friends can then do the same to you.
Let’s say that each of your two friends have two other friends who want their certificates signed. If your two friends sign these other certificates, then you can use the trust that you have in your friends to accept that these other people are truly who they say they are as well.
The friends of your friends can then sign the certificates of the people that they trust and so on, eventually building a large network of individuals that are trusted. Once these webs get big enough and become interconnected with other webs, they can be used as a means to trust anyone else in the network.
The more signatures on a certificate, especially if they are signatures from highly trusted individuals, the more you can trust someone’s digital certificate and the link between their public key and their identity.
PGP users frequently hold key-signing parties where people congregate in order to have their identities checked and their digital certificates signed. These gatherings help to bring new people into the network.
Although it comes with some complexities, the advantage of the web of trust system is that there is no central body that can be corrupted.
Are digital signatures safe?
In a general sense, digital signatures are secure unless the private key of the signee has been compromised. If the owner has informed another person, left the private key written down, or had it stolen in another way, then it is possible for an attacker to digitally sign messages as if they were the owner.
This can lead to the attacker impersonating their victim or tampering with their data. This is a huge security issue, and anyone who suspects that their key has been compromised must revoke their digital certificate that links them to their public key, and have a new one issued.
There are a few other caveats when it comes to the security of digital signatures. An appropriate digital signature algorithm should be used, and it also needs to be implemented properly. Alongside this, there also needs to be a way of linking the public key to its owner, usually through digital certificates.
As long as these requirements are met, you are following industry best practices, and your private key has not been compromised, then digital signatures are an excellent way to provide authenticity, integrity and non-repudiation to data.


I am pretty much pleased with your good work. You put really very helpful information.sharing this sort of educational posts.
Digital Signature Certificate